
【题目】(2016.镇江)如图,AD、BC相交于点O,AD=BC,∠C=∠D=90°.
(1)若∠ABC=35°,求∠CAO的度数;
(2)求证:CO=DO

【答案】(1)20°;(2)见解析;
【解析】(1)根据HL证明Rt△ABC≌Rt△BAD;由全等的性质得∠BAD=∠ABC,根据直角三角形两直角互余可求∠BAC=55 ,从而可求出∠CAO的度数;
(2)利用全等三角形的性质可得∠BAD=∠ABC,BC=AD,从而可证求证CO=DO.
∵∠D=∠C=90°,
∴△ABC和△BAD都是Rt△,
在Rt△ABC和Rt△BAD中,
∵AD=BC,AB=BA,
∴Rt△ABC≌Rt△BAD(HL);
∴∠BAD=∠ABC=35°.
∵∠ABC=35°,
∴∠BAC=90-35=55,
∴∠CAO=55-35=20.
(2)证明:∵Rt△ABC≌Rt△BAD,
∴∠BAD=∠ABC,BC=AD,
∴AO=BO,
∴BC-BO=AD-AO,
∴CO=DO.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC. 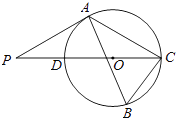
(1)求证:PA是⊙O的切线;
(2)若AB=4+ ![]() ,BC=2
,BC=2 ![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点N,连接BM,DN.

(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC与BD相交于O,∠1=∠4,∠2=∠3,△ABC的周长为25cm,△AOD的周长为17cm,则AB=( )
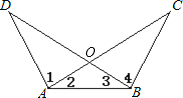
A. 4cm ; B. 8cm; C. 12cm; D. 无法确定;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠B=∠DEF,AB=DE,要说明△ABC≌△DEF.(1)若以“ASA”为依据,还缺条件 _________________ ;(2)若以“AAS”为依据,还缺条件___________________;(3)若以“SAS”为依据,还缺条件___________________;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是射线CB上的一动点(不与点B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段CB上,且∠BAC=90°时,那么∠DCE= 度;
(2)设∠BAC= ![]() ,∠DCE=
,∠DCE= ![]() .
.
① 如图2,当点D在线段CB上,∠BAC≠90°时,请你探究![]() 与
与![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
② 如图3,当点D在线段CB的延长线上,∠BAC≠90°时,请将图3补充完整,并直接写出此时![]() 与
与![]() 之间的数量关系(不需证明).
之间的数量关系(不需证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD中,F是AB上一点,H是BC延长线上一点,连接FH,将△FBH沿FH翻折,使点B的对应点E落在AD上,EH与CD交于点G,连接BG交FH于点M,当GB平分∠CGE时,BM=2![]() ,AE=8,则ED=______.
,AE=8,则ED=______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有A、B两个点.
(1)如图1,若AB=a,M是AB的中点,C为线段AB上的一点,且![]() ,则AC= ,CB= ,MC= (用含a的代数式表示);
,则AC= ,CB= ,MC= (用含a的代数式表示);
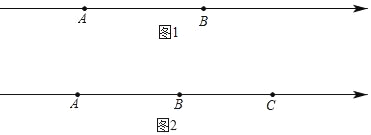
(2)如图2,若A、B、C三点对应的数分别为﹣40,﹣10,20.
①当A、C两点同时向左运动,同时B点向右运动,已知点A、B、C的速度分别为8个单位长度/秒、4个单位长度/秒、2个单位长度/秒,点M为线段AB的中点,点N为线段BC的中点,在B、C相遇前,在运动多少秒时恰好满足:MB=3BN.
②现有动点P、Q都从C点出发,点P以每秒1个单位长度的速度向终点A移动;当点P移动到B点时,点Q才从C点出发,并以每秒3个单位长度的速度向左移动,且当点P到达A点时,点Q也停止移动(若设点P的运动时间为t).当PQ两点间的距离恰为18个单位时,求满足条件的时间t值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)45+(﹣20);
(2)(﹣8)﹣(﹣1);
(3)|﹣10|+|+8|;
(4)(﹣12)﹣5+(﹣14)﹣(﹣39);
(5)0.47﹣4![]() ﹣(﹣1.53)﹣1
﹣(﹣1.53)﹣1![]() ;
;
(6)36﹣76+(﹣23)﹣105;
(7)﹣20+|﹣14|﹣(﹣18)﹣13;
(8)(+1.75)+(﹣![]() )+(+
)+(+![]() )+(+1.05)+(﹣
)+(+1.05)+(﹣![]() )+(+2.2).
)+(+2.2).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com