Question

【题目】如图，△ABC内接于⊙O，∠B=60°，CD是⊙O的直径，点P是CD延长线上的一点，且AP=AC．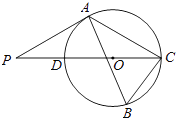

（1）求证：PA是⊙O的切线；
（2）若AB=4+ ，BC=2 ，求⊙O的半径．

Answer 1

【答案】
（1）证明：连接OA，

∵∠B=60°，

∴∠AOC=2∠B=120°，

又∵OA=OC，

∴∠OAC=∠OCA=30°，

又∵AP=AC，

∴∠P=∠ACP=30°，

∴∠OAP=∠AOC﹣∠P=90°，

∴OA⊥PA，

∴PA是⊙O的切线

（2）解：过点C作CE⊥AB于点E．

在Rt△BCE中，∠B=60°，BC=2 ，

∴BE= BC= ，CE=3，

∵AB=4+ ，

∴AE=AB﹣BE=4，

∴在Rt△ACE中，AC= =5，

∴AP=AC=5．

∴在Rt△PAO中，OA= ，

∴⊙O的半径为 ．

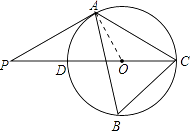
【解析】（1）连接OA，根据圆周角定理求出∠AOC，再由OA=OC得出∠ACO=∠OAC=30°，再由AP=AC得出∠P=30°，继而由∠OAP=∠AOC﹣∠P，可得出OA⊥PA，从而得出结论；（2）过点C作CE⊥AB于点E．在Rt△BCE中，∠B=60°，BC=2 ，于是得到BE= BC= ，CE=3，根据勾股定理得到AC= =5，于是得到AP=AC=5．解直角三角形即可得到结论．