
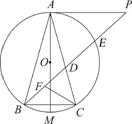
如图,⊙O是△ABC的外接圆,P是⊙O外的一点,AM是⊙O的直径,∠PAC=∠ABC
(1) 求证:PA是⊙O的切线;
(2) 连接PB与AC交于点D,与⊙O交于点E,F为BD上的一点,若M为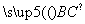 的中点,且∠DCF=∠P,求证:
的中点,且∠DCF=∠P,求证: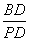 =
= 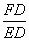 =
= 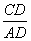 .
.
科目:初中数学 来源: 题型:
4.两名同学进行了10次三级蛙跳测试,经计算,他们的平均成绩相同,若要比较这两名同学的成绩哪一位更稳定,通常还需要比较他们的成绩的( )
(A)众数 (B)中位数 (C)方差 (D)以上都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
小明随机调查了若干市民租用公共自行车的骑车时间t(单位:分),将获得的数据分成四组,绘制了如下统计图。请根据图中信息,解答下列问题:
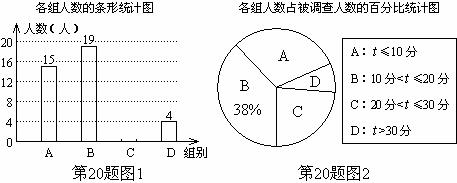
(1)这次被调查的总人数是多少?
(2)试求表示A组的扇形圆心角的度数,并补全条形统计图;
(3)如果骑自行车的平均速度为12km/h,请估算,在租用公共自行车的市民中,骑车路程不超过6km的人数所占的百分比。21·cn·jy·com
查看答案和解析>>
科目:初中数学 来源: 题型:
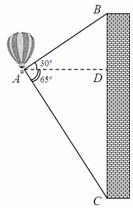
如图,热气球的探测器显示,从热气球A处看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为65°,热气球与高楼的水平距离AD为120m.求这栋高楼的高度. (结果用含非特殊角的三角函数及根式表示即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
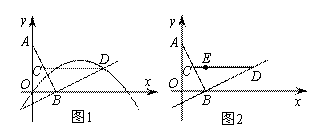
已知在平面直角坐标系xOy中,O为坐标原点,线段AB的两个端点A(0,2),B(1,0)分别在y轴和x轴的正半轴上,点C为线段AB的中点,现将线段BA绕点B按顺时针方向旋转90°得到线段BD,抛物线y=ax2+bx+c(a≠0)经过点D
1) 如图1,若该抛物线经过原点O,且a=−
① 求点D的坐标及该抛物线的解析式
② 连结CD,问:在抛物线上是否存在点P,使得∠POB与∠BCD互余?若存在,请求出所有满足条件的点P的坐标,若不存在,请说明理由
2) 如图2,若该抛物线y=ax2+bx+c(a≠0)经过点E(1,1),点Q在抛物线上,且满足∠QOB与∠BCD互余,若符合条件的Q点的个数是4个,请直接写出a的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com