
【题目】如图,⊙O经过点B,D,E,BD是⊙O的直径,∠C=90°,BE平分∠ABC.
(1)证明:直线AC是⊙O的切线.
(2)当AE=4,AD=2时,求⊙O的半径.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】有一个直径为1m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC,如图所示.
(1)求被剪掉阴影部分的面积:
(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲和乙同时从学校放学,两人以各自送度匀速步行回家,甲的家在学校的正西方向,乙的家在学校的正东方向,乙家离学校的距离比甲家离学校的距离远3900米,甲准备一回家就开始做什业,打开书包时发现错拿了乙的练习册.于是立即步去追乙,终于在途中追上了乙并交还了练习册,然后再以先前的速度步行回家,(甲在家中耽搁和交还作业的时间忽略不计)结果甲比乙晚回到家中,如图是两人之间的距离y米与他们从学校出发的时间x分钟的函数关系图,则甲的家和乙的家相距_____米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=8,AC=5,AD是∠BAC的角平分线,点D在△ABC内部,连接AD、BD、CD,∠ADB=150°,∠DBC=30°,∠ABC+∠ADC=180°,则线段CD的长度为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学课上,老师在屏幕上出示了一个例题:在△ABC中,D,E分别是AB,AC上的一点,BE与CD交于点O,画出图形(如图),给出下列四个条件:①∠DBO=∠ECO;②∠BDO=∠CEO;③BD=CE;④OB=OC.

(1)要求同学从这四个等式中选出两个作为已知条件,可判定△ABC是等腰三角形.
请你用序号在横线上写出所有情形.答:
(2)选择第(1)题中的一种情形,说明△ABC是等腰三角形的理由,并写出解题过程.
解:我选择 .
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
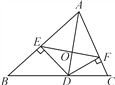
【题目】如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下面四个结论:①OA=OD;②AD⊥EF;③当∠BAC=90°时,四边形AEDF是正方形;④AE2+DF2=AF2+DE2.其中正确的是_________.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙3名学生各自随机选择到A、B 2个书店购书.
(1)求甲、乙2名学生在不同书店购书的概率;
(2)求甲、乙、丙3名学生在同一书店购书的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,![]() ,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
(1)求∠BAC的度数;
(2)当点D在AB上方,且CD⊥BP时,求证:PC=AC;
(3)在点P的运动过程中
①当点A在线段PB的中垂线上或点B在线段PA的中垂线上时,求出所有满足条件的∠ACD的度数;
②设⊙O的半径为6,点E到直线l的距离为3,连结BD,DE,直接写出△BDE的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com