Question

【题目】如图(1)，AB=4cm，AC⊥AB于A，BD⊥AB于B，AC=BD=3cm.点P在线段AB上以lcm/s的速度由点A向点B运动，同时，点Q在线段BD上由点B向点D运动．它们运动的时间为t(s)．

(1)若点Q的运动速度与点P的运动速度相等，当t=l时，△ACP与△BPQ是否全等？PC与PQ是否垂直？请分别说明理由；

(2)如图(2)，将图(1)中的“AC上AB于A,BD上AB于B”改为“∠CAB=∠DBA=60”，其他条件不变.设点Q的运动速度为x cm/s，是否存在实数x，使得△ACP与△BPQ全等?若存在，求出相应的x、t的值；若不存在，请说明理由.

Answer 1

【答案】(1) △ACP≌△BPQ，PC垂直于PQ,理由见解析.(2)存在，见解析.

【解析】试题分析：（1）利用SAS证得△ACP≌△BPQ，得出∠ACP=∠BPQ，进一步得出∠APC+∠BPQ=∠APC+∠ACP=90°得出结论即可；
（2）由△ACP≌△BPQ，分两种情况：①AC=BP，AP=BQ，②AC=BQ，AP=BP，建立方程组求得答案即可．

试题解析：(1)当t=1时，△ACP≌△BPQ，PC垂直于PQ

理由如下：

当t=1时，AP=BQ=1，BP=AC=3，
又∠A=∠B=90°，
∴在△ACP和△BPQ中，

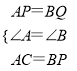
∴△ACP≌△BPQ．
∴∠ACP=∠BPQ，
∴∠APC+∠BPQ=∠APC+∠ACP=90°．
∴∠CPQ=90°，即线段PC与线段PQ垂直．
（2）①若△ACP≌△BPQ，
则AC=BP，AP=BQ，

解得

②若△ACP≌△BQP，
则AC=BQ，AP=BP，

解得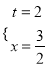

综上所述，存在或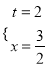使得△ACP与△BPQ全等．