
【题目】如图,已知∠DAB+∠D=180°,AC平分∠DAB,且∠CAD=25°,∠B=95°.求:∠DCE和∠DCA的度数.

请将以下解答补充完整,
解:因为∠DAB+∠D=180°
所以DC∥AB__________
所以∠DCE=∠B__________
又因为∠B=95°,
所以∠DCE=________°;
因为AC平分∠DAB,∠CAD=25°,根据角平分线定义,
所以∠CAB=________=________°,
因为DC∥AB
所以∠DCA=∠CAB,__________
所以∠DCA=________°.
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,对正方形ABCD及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘同一实数a,将得到的点先向右平移m个单位长度,再向上平移n个单位长度(m>0,n>0),得到正方形A′B′C′D′及其内部的点,其中点A,B的对应点分别为A′,B′.已知正方形ABCD内部的一个点F经过上述操作后得到的对应点F′与点F重合,求点F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天数学课上老师讲了整式的加减运算,小颖回家后拿出自己的课堂笔记,认真地复习老师在课堂上所讲的内容,她突然发现一道题目:5(2a2+3ab-b2)-(-3+ab+5a2+b2)=5a2■-6b2+3被墨水弄脏了,请问被墨水遮盖住的一项是()
A.+14abB.+3abC.+16abD.+2ab
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),AB=4cm,AC⊥AB于A,BD⊥AB于B,AC=BD=3cm.点P在线段AB上以lcm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).

(1)若点Q的运动速度与点P的运动速度相等,当t=l时,△ACP与△BPQ是否全等?PC与PQ是否垂直?请分别说明理由;
(2)如图(2),将图(1)中的“AC上AB于A,BD上AB于B”改为“∠CAB=∠DBA=60![]() ”,其他条件不变.设点Q的运动速度为x cm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
”,其他条件不变.设点Q的运动速度为x cm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G,H,交BD于点O.
(1)求证:△ABE≌△CDF;
(2)连接DG,若DG=BG,则四边形BEDF是什么特殊四边形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张矩形纸片,剪下一个正方形,剩下一个矩形,称为第一次操作;在剩下的矩形纸片中再剪下一个正方形,剩下一个矩形,称为第二次操作;…;若在第n次操作后,剩下的矩形为正方形,则称原矩形为n阶奇异矩形.
(1)如图1,矩形ABCD中,若AB=3,BC=9,则称矩形ABCD为 阶奇异矩形.
(2)如图2,矩形ABCD长为7,宽为3,它是奇异矩形吗?如果是,请写出它是几阶奇异矩形,并在图中画出裁剪线;如果不是,请说明理由.
(3)已知矩形ABCD的一边长为20,另一边长为a(a<20),且它是3阶奇异矩形,请画出矩形ABCD及裁剪线的示意图,并在图的下方直接写出a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
(1)△BEF是等腰三角形吗?试说明理由;
(2)若AB=4,AD=8,求CF的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
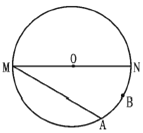
【题目】如图,MN是⊙O的直径,MN=4,点A在⊙O上,∠AMN=30°,B为![]() 的中点,P是直径MN上一动点.
的中点,P是直径MN上一动点.
(1)利用尺规作图,确定当PA+PB最小时P点的位置(不写作法,但要保留作图痕迹).
(2)求PA+PB的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com