
����Ŀ��һ�ž���ֽƬ������һ�������Σ�ʣ��һ�����Σ���Ϊ��һ�β�������ʣ�µľ���ֽƬ���ټ���һ�������Σ�ʣ��һ�����Σ���Ϊ�ڶ��β������������ڵ�n�β�����ʣ�µľ���Ϊ�����Σ����ԭ����Ϊn��������Σ�
��1����ͼ1������ABCD�У���AB=3��BC=9����ƾ���ABCDΪ������������Σ�
��2����ͼ2������ABCD��Ϊ7����Ϊ3�������������������ǣ���д�����Ǽ���������Σ�����ͼ�л����ü��ߣ�������ǣ���˵�����ɣ�
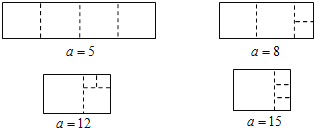
��3����֪����ABCD��һ�߳�Ϊ20����һ�߳�Ϊa��a��20����������3��������Σ��뻭������ABCD���ü��ߵ�ʾ��ͼ������ͼ���·�ֱ��д��a��ֵ��

���𰸡���1��2 ��2������ABCD��4��������� ��3��ͼ�μ�����
�������������������1����֪����2�β�����ʣ�µľ���Ϊ�����Σ� ���Ծ���ABCDΪ2���������. ��1��������֪�������軭�����ɣ���2��������֪�ó�������������4�����������ͼ�μ��ɣ�
�⣺��1������2�β�����ʣ�µľ���Ϊ�����Σ�
�� ����ABCDΪ2���������
��2������ABCD��4��������Σ��ü��ߵ�ʾ��ͼ���£�

��3���ü��ߵ�ʾ��ͼ���£�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(��ͼ����O����ABC�����Բ��Բ��O��AB�ϣ�����B��2��A��M��OA��һ�㣬��M��AB�Ĵ��߽�AC�ڵ�N����BC���ӳ����ڵ�E��ֱ��CF��EN�ڵ�F��EF��FC.
(1)��֤��CF����O�����ߣ�
(2)����O�İ뾶Ϊ2����AC��CE����AM�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ5��OΪֱ��AB��һ�㣬 ��AOC=48��,OEƽ�֡�AOC, ��DOE=90��
(1)���BOE�Ķ�����
(2)���ж�OD�Ƿ�ƽ�֡�BOC����˵�����ɡ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��DAB+��D=180�㣬ACƽ����DAB������CAD=25�㣬��B=95��������DCE����DCA�Ķ�����

�뽫���½��������
�⣺��Ϊ��DAB+��D=180��
����DC��AB__________
������DCE=��B__________
����Ϊ��B=95�㣬
������DCE=________�㣻
��ΪACƽ����DAB����CAD=25�������ݽ�ƽ���߶��壬
������CAB=________=________�㣬
��ΪDC��AB
������DCA=��CAB��__________
������DCA=________�㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Ľ�����̵ĺ�������գ�����������ע������
.��ͼ����֪��A=��F����C=��D����˵��BD��CE.

�⣺�ߡ�A=��F(��֪)
��AC��DF( )
���D=�� ( )
���ߡ�C=��D(��֪)
���1=��C(��������)
��BD��CE( )
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ�����������ʶ�IJ������룬�ϴ����˹ѧ������![]() ��������������������֤����������
��������������������֤����������![]() ����������ô�����������ʵ�������p��q��ʹ��
����������ô�����������ʵ�������p��q��ʹ��![]() ������
������![]() ������ƽ����p2=2q2 �� ��Ϊ2q2��ż��������p2��ż������ֻ��ż����ƽ������ż��������pҲ��ż������˿���p=2s��������ʽ����4s2=2q2 �� ��q2=2s2 �� ����qҲ��ż����������p��q����ż���������ʣ��������p��q����ì�ܣ����ì��˵����
������ƽ����p2=2q2 �� ��Ϊ2q2��ż��������p2��ż������ֻ��ż����ƽ������ż��������pҲ��ż������˿���p=2s��������ʽ����4s2=2q2 �� ��q2=2s2 �� ����qҲ��ż����������p��q����ż���������ʣ��������p��q����ì�ܣ����ì��˵���� ![]() ����д�ɷ�������ʽ����
����д�ɷ�������ʽ����![]() ���������������������Ƶķ�����֤��
���������������������Ƶķ�����֤��![]() ������������
������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A��B������ֱ�ΪA��-4��0����B��2��0������C��y���ϣ��ҡ�ABC�����Ϊ6���Ե�A��B��CΪ��������ABCD.����ԭ���ֱ��ƽ�ָ���ABCD����������ֱ�ߵĽ���ʽ��________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���C=90����BC=8cm��AC=6cm����E��BC���е㣬����P��A�����������ÿ��2cm���ٶ���A��C�˶���Ȼ����1cm/s���ٶ���C��B�˶��������P�˶���ʱ����t�룬��ô��t=_______����APE���������8��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com