
����Ŀ�����ͬѧ���䷽���Ƶ�һԪ���η���ax2+bx+c=0��a��0���������ʽʱ������b2��4ac��0������������������ģ�
����a��0������ax2+bx+c=0������
x2+![]() x=��
x=��![]() ������һ��
������һ��
x2+![]() x+��
x+��![]() ��2=��
��2=��![]() +��
+��![]() ��2�����ڶ���
��2�����ڶ���
��x+![]() ��2=
��2=![]() ����������
����������
x+![]() =
=![]() ��b2��4ac��0���������IJ�
��b2��4ac��0���������IJ�
x=![]() �������岽
�������岽
��俵Ľⷨ�ӵ���������ʼ���ִ�����ʵ�ϣ���b2��4ac��0ʱ������ax2+bx+c=0��a��O���������ʽ��������
���䷽���ⷽ�̣�x2��2x��24=0��
 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������·һ��װ������һ�ֽ���Ϊ50Ԫ/���ij��£��������ҹ涨ÿ������Ϊ60��150Ԫ��������Ϊ60Ԫ/��ʱ��ÿ���ڿ�����70����ÿ��ÿ�Ǽ�10Ԫ��һ����������5����
(1)��ÿ�����¶���Ϊ����Ԫʱ(����Ϊ10Ԫ����������)����װ��ÿ���ڵ���������������Ϊ����Ԫ��
(2)�����ÿ�����µĶ������ĸ���Χ��ʱ��ÿ���ڵ�����������2 700Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��ʾ������ABC�У���C=90�㣬BC=5cm��AC=7cm����������P��Q�ֱ��B��C����ͬʱ���������е�P��1����/����ٶ������߶�BC���C�˶�����Q��2����/����ٶ������߶�CA���A�˶���
��1��P��Q�������˶������У������������PCQ���������4����2�����������PQ�ij��ȵ���5���ף�
��2����P��Q�������˶������У��ı���ABPQ������ܷ����11����2����˵�����ɣ�
��3����������ʱ��C��P��QΪ���������������ABC���ƣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ھ���ֽƬABCD�У�AB=3cm��AD=5cm���۵�ֽƬʹB�����ڱ�AD�ϵ�E�����ۺ�ΪPQ������E��EF��AB��PQ��F������BF��
��1����֤���ı���BFEPΪ���Σ�
��2������E��AD�����ƶ�ʱ���ۺ۵Ķ˵�P��QҲ��֮�ƶ���
�ٵ���Q���C�غ�ʱ����ͼ2����������BFEP�ı߳���
������P��Q�ֱ��ڱ�BA��BC���ƶ��������E�ڱ�AD���ƶ��������룮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶��500��ѧ�������������ȡ��һ����ѧ����ͳ��ÿ��д��ҵ��ʱ�䣬�������ǵ�ʱ��(��λ������)�����Ƴ����µ�ͳ��ͼ����ͼ������������Ϣ������������⣺

(1)ͼ����m=________��n=________��
(2)��ͳ�Ƶ��������ݵ�ƽ��������������λ����
(3)�����������ݣ�������500��ѧ���У�ʱ��Ϊ120���ӵ�Լ�ж���ѧ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ʒ�Ľ���Ϊÿ��40Ԫ�����ۼ�Ϊÿ��60Ԫʱ��ÿ���ڿ�����300�������轵�۴������Ҿ��г����飺ÿ����1Ԫ��ÿ���ڿɶ�����20��������Ҫʹÿ��������Ϊ6125Ԫ����ÿ����ƷӦ����xԪ������з���Ϊ(����)
A. (20��x)(300��20x)��6125 B. (20��x)(300��20x)��6125
C. (20��x)(300��20x)��6125 D. (20��x)(300��20x)��6125
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵȱ�![]() �У�
�У�![]() ���ף�
���ף�![]() ���ף������
���ף������![]() ��
��![]() ����
����![]() ���ٶ��˶���
���ٶ��˶���

��1�������![]() ���߶�
���߶�![]() ���ɵ�
���ɵ�![]() ���
���![]() �˶�����
�˶�����![]() ���߶�
���߶�![]() ����
����![]() ����
����![]() ���˶�������ͬʱ����������
���˶�������ͬʱ����������![]() ���˶��ٶ����
���˶��ٶ����![]() ���˶��ٶ���ȣ�
���˶��ٶ���ȣ�
�پ�����![]() ���
���![]() ��
��![]() �Ƿ�ȫ�ȣ���˵�����ɣ�
�Ƿ�ȫ�ȣ���˵�����ɣ�
�ڵ�������˶�ʱ��Ϊ������ʱ��![]() �պ���һ��ֱ�������Σ�
�պ���һ��ֱ�������Σ�
��2������![]() ���˶��ٶ����
���˶��ٶ����![]() ���˶��ٶȲ���ȣ���
���˶��ٶȲ���ȣ���![]() �ӵ�
�ӵ�![]() ��������
��������![]() ��ԭ�����˶��ٶȴӵ�
��ԭ�����˶��ٶȴӵ�![]() ͬʱ��������˳ʱ����
ͬʱ��������˳ʱ����![]() �����˶�������
�����˶�������![]() ��ʱ��
��ʱ��![]() ���
���![]() ��һ�����������
��һ�����������![]() ���˶��ٶ���__________����
���˶��ٶ���__________����![]() �룮��ֱ��д���𰸣�
�룮��ֱ��д���𰸣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
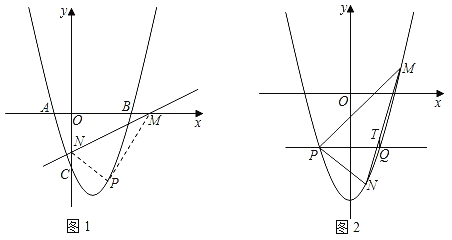
����Ŀ����֪������y��ax2��2ax��3a��y�ύ��C�㣬��x����A��B����OB��OC��
��1���������ߵĽ���ʽ��
��2����ͼ1��ֱ��l��y��![]() x+b��b��0����x����M����y����N������MON��ֱ��l���ۣ��õ���MPN����O�Ķ�Ӧ��ΪP����O�Ķ�Ӧ��Pǡ�������������ϣ���ֱ��l�Ľ���ʽ��
x+b��b��0����x����M����y����N������MON��ֱ��l���ۣ��õ���MPN����O�Ķ�Ӧ��ΪP����O�Ķ�Ӧ��Pǡ�������������ϣ���ֱ��l�Ľ���ʽ��
��3����ͼ2����ԭ����������ƽ��1����λ������ƽ��t����λ���õ���������C1����ֱ��y��m����������C1����P��Q���㣬��M����������C1��һ���㣬����PM������ֱ��PM��y��m���۽���������C1��N����Q��QT��y�ᣬ��MN�ڵ�T����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ȫ��ͬ��С�����ų�һ������Σ�AB������һ��С���εĶԽ��ߣ����ڴ������������л�ͼ��Ҫ�ٽ����̶�ֱ�ߢڱ�����Ҫ����ͼ�ۼ�.
(1)����ͼ�л������߶�ABƽ�е��߶�CD
(2)����ͼ�л�������A���߶�AB��ֱ���߶�AE
(3)����ͼ�л����߶�AB�Ĵ�ֱƽ����MN


�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com