
【题目】江汉路一服装店销售一种进价为50元/件的衬衣,生产厂家规定每件定价为60~150元.当定价为60元/件时,每星期可卖出70件,每件每涨价10元,一星期少卖出5件.
(1)当每件衬衣定价为多少元时(定价为10元的正整数倍),服装店每星期的利润最大?最大利润为多少元?
(2)请分析每件衬衣的定价在哪个范围内时,每星期的销售利润不低于2 700元.
【答案】 (1)当每件衬衣定价为120元或130元时,服装店每星期的利润最大,最大利润为2 800元.
(2)每件衬衣的定价在110~140元之间时(定价为10元的正整数倍),每星期的销售利润不低于2 700元.
【解析】试题分析:(1)设每件衬衣定价为x元,服装店每星期的利润为W元,利用每一件的利润乘卖出的件数列出二次函数,利用二次函数的性质即可解决问题;(2)根据(2)中求出的二次函数,建立一元二次方程求出方程的解,确定出涨价最少时的x的值,根据二次函数的性质即可求得x的取值范围.
试题解析:
(1)设每件衬衣定价为x元,服装店每星期的利润为W元.由题意得,
W=(x-50)![]() =-
=-![]() x2+125x-5 000=-
x2+125x-5 000=-![]() (x-125)2+2 812.5.
(x-125)2+2 812.5.
∵60≤x≤150,且x是10的正整数倍,
∴当x取120或130时,W有最大值2 800.因此,当每件衬衣定价为120元或130元时,服装店每星期的利润最大,最大利润为2 800元.
(2)令W=2 700,
即-![]() x2+125x-5 000=2 700,
x2+125x-5 000=2 700,
解得x1=110,x2=140.
∴每件衬衣的定价在110~140元之间时(定价为10元的正整数倍),每星期的销售利润不低于2 700元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,D为BC边的中点,过点B作BF⊥AB交AD的延长线于点F,CE平分∠ACB交AD于点E.
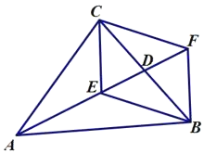
(1)判断四边形CEBF的形状,并证明;
(2)若AD=![]() ,求BF及四边形CEBF的面积.
,求BF及四边形CEBF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C、D是⊙O上的两点,且AC=CD.
(1)求证:OC∥BD;
(2)若BC将四边形OBDC分成面积相等的两个三角形,试确定四边形OBDC的形状.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料,并解答相应的问题:
幻方
将若干个数组成一个正方形数阵,若任意一行,一列及对角线上的数字之和都相等,则称具有这种性质的数字方阵为“幻方”.中国古代称“幻方”为“河图”、“洛书”等.例如,下面是三个三阶幻方,是将数字1,2,3,4,5,6,7,8,9填入到3×3的方格中得到的,其每行、每列、每条对角线上的三个数之和相等.

(1)设下面的三阶幻方中间的数字是x(其中x为正整数),请用含x的代数式将下面的幻方填充完整.
x+3 | x﹣4 | |
x﹣2 | x | |
x﹣1 | x﹣3 |
(2)若设(1)题幻方中9个数的和为S,则S与中间的数字x之间的数量关系为 .
(3)请在下面的A、B两题中任选一题作答,我选择 .
现要用9个数3,4,5,6,7,8,9,10,11构造一个三阶幻方.
A、幻方最中间的数字应等于 .
B、请将构造的幻方填写在下面3×3的方格中.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解九年级学生体育测试情况,以九年级(1)班学生的体育测试成绩为样本,按A,B,C,D四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题:

(说明:A级:90分~100分;B级:75分~89分;C级:60分~74分;D级:60分以下)
(1)请把条形统计图补充完整;
(2)扇形统计图中D级所在的扇形的圆心角度数是多少?
(3)若该校九年级有600名学生,请用样本估计体育测试中A级学生人数约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天一个巡警骑摩托车在一条南北大道上巡逻,他从岗亭出发,在某个时刻停留在A处,规定以岗亭为原点,向北方向为正,这段时间行驶纪录如下(单位:千米)
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)![]() 在岗亭哪个方向?距岗亭多远?
在岗亭哪个方向?距岗亭多远?
(2)若摩托车行驶每千米耗油![]() 升,每升
升,每升![]() 元,且最后返回岗亭,这一天耗油共需多少元?
元,且最后返回岗亭,这一天耗油共需多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABC中,AB=5,AC=12,BC=13,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为( )
ABC中,AB=5,AC=12,BC=13,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在0,3.14,![]() ,2π,-
,2π,-![]() ,
,![]() ,-0.4,-
,-0.4,-![]() ,4.262262226…(每两个”6”之间依次多一个”2”)中,
,4.262262226…(每两个”6”之间依次多一个”2”)中,
属于有理数的有_________________________________________________;
属于无理数的有________________________________________________________;
属于正实数的有_________________________________________________________;
属于负实数的有_____________________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇同学用配方法推导一元二次方程ax2+bx+c=0(a≠0)的求根公式时,对于b2﹣4ac>0的情况,她是这样做的:
由于a≠0,方程ax2+bx+c=0变形为:
x2+![]() x=﹣
x=﹣![]() ,…第一步
,…第一步
x2+![]() x+(
x+(![]() )2=﹣
)2=﹣![]() +(
+(![]() )2,…第二步
)2,…第二步
(x+![]() )2=
)2=![]() ,…第三步
,…第三步
x+![]() =
=![]() (b2﹣4ac>0),…第四步
(b2﹣4ac>0),…第四步
x=![]() ,…第五步
,…第五步
嘉淇的解法从第 步开始出现错误;事实上,当b2﹣4ac>0时,方程ax2+bx+c=0(a≠O)的求根公式是 .
用配方法解方程:x2﹣2x﹣24=0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com