
|
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
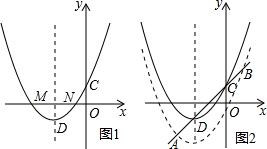
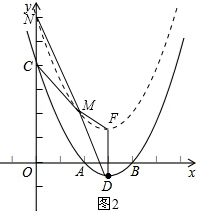 CN=DF=2.如图2,
CN=DF=2.如图2,| 1 |
| 2 |
|
|
| 1 |
| 2 |
|
|
|
|
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
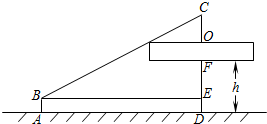 如图,一桥梁建设工地上有一架吊车,底座高AB=1.5米,吊臂长BC=18米,它与地面保持成30°角,现要将一个底面圆直径为8米,高为2米的圆柱体的钢筋混凝土框架,安装到离地面高度为6米的桥基上,问这架吊车能否完成这安装任务?请说明理由.(说明:图中钢索CO吊在长方体框架的上底面的中心处)
如图,一桥梁建设工地上有一架吊车,底座高AB=1.5米,吊臂长BC=18米,它与地面保持成30°角,现要将一个底面圆直径为8米,高为2米的圆柱体的钢筋混凝土框架,安装到离地面高度为6米的桥基上,问这架吊车能否完成这安装任务?请说明理由.(说明:图中钢索CO吊在长方体框架的上底面的中心处)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com