
����Ŀ��Ϊ�˸��õر���������ij����ˮ�����������ȹ���A��B������ˮ�����豸��20̨�����ܱ���ˮ���д�����ÿ̨A����ˮ�����豸12��Ԫ��ÿ̨B����ˮ�����豸10��Ԫ����֪2̨A����ˮ�����豸��1̨B����ˮ�����豸ÿ�ܿ��Դ�����ˮ680�֣�4̨A����ˮ�����豸��3̨B����ˮ�����豸ÿ�ܿ��Դ�����ˮ1560�֣�
��1����A��B������ˮ�����豸ÿ��ÿ̨�ֱ���Դ�����ˮ���ٶ֣�
��2����Ԥ�㣬����ˮ�����������豸���ʽ���230��Ԫ��ÿ�ܴ�����ˮ����������4500�֣������оٳ����й�����
��3��������dz������ӽ�Լ�ʽ�ĽǶ���̸̸���ѡ�����ַ�����˵�����ɣ�
���𰸡�
��1���⣺��A����ˮ�����豸ÿ��ÿ̨���Դ�����ˮx�֣�B����ˮ�����豸ÿ��ÿ̨���Դ�����ˮy�֣�
![]() ��
��
��ã� ![]()
��A����ˮ�����豸ÿ��ÿ̨���Դ�����ˮ240�֣�B����ˮ�����豸ÿ��ÿ̨���Դ�����ˮ200�֣�
��2���⣺�蹺��A����ˮ�����豸ą������B����ˮ�����豸��20��a��̨��
�� ![]() ��
��
��ã�12.5��x��15��
��һ�ַ�������a=13ʱ��20��a=7��������A����ˮ�����豸13̨������B����ˮ�����豸7̨��
�ڶ��ַ�������a=14ʱ��20��a=6��������A����ˮ�����豸14̨������B����ˮ�����豸6̨��
�����ַ�������a=15ʱ��20��a=5��������A����ˮ�����豸15̨������B����ˮ�����豸5̨
��3���⣺������dz������ӽ�Լ�ʽ�ĽǶȿ��ǣ��һ�ѡ���һ�ַ�����������A����ˮ�����豸13̨������B����ˮ�����豸7̨��
��Ϊ��һ�ַ��������ʽ�13��12+7��10=226��Ԫ��
�ڶ��ַ��������ʽ�14��12+6��10=228��Ԫ��
�����ַ��������ʽ�15��12+5��10=230��Ԫ��
��226��228��230��
��ѡ���һ�ַ��������ʽ����٣�������226��Ԫ
����������1������2̨A����ˮ�����豸��1̨B����ˮ�����豸ÿ�ܿ��Դ�����ˮ680�֣�4̨A����ˮ�����豸��3̨B����ˮ�����豸ÿ�ܿ��Դ�����ˮ1560�֣������г���Ӧ�Ķ�Ԫһ�η����飬�Ӷ�����⣻��2������3��������������г���Ӧ�IJ���ʽ�飬�Ӷ����Եõ��������Ӷ��������ÿ�ַ��������ʽ𣬴Ӷ����Խ���⣮
�����㾫����������Ĺؼ���������һԪһ�β���ʽ���Ӧ�õ����֪ʶ������1���������⣬�ҳ����ȹ�ϵ��2���裺��δ֪����3���У��г�����ʽ�飻4���⣺�ⲻ��ʽ�飻5�����飺�Ӳ���ʽ��Ľ⼯���ҳ���������Ĵ𰸣�6����д������𰸣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Ҫ����
��1�����㣺5a2b�£��� ![]() ab����2ab2��2
ab����2ab2��2
��2�����㣺20142��2013��2015
��3����ʽ�ֽ⣺a2��x��y��+4b2��y��x����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������8�֣�ijҩƷ�о�������һ�ֿ�����ҩ�������궯��ʵ�飬�״������ٴ�����ʵ�飮��ó��˷�ҩ��ѪҺ��ҩ�����![]() ����/���������ҩʱ��
����/���������ҩʱ��![]() Сʱ֮��ĺ�����ϵ��ͼ��ʾ����
Сʱ֮��ĺ�����ϵ��ͼ��ʾ����![]() ʱ��
ʱ��![]() ��
��![]() �ɷ��ȣ���
�ɷ��ȣ���

��1������ͼ��ֱ����ѪҺ��ҩ��Ũ���������½���![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��2����ѪҺ��ҩ��Ũ�Ȳ�����4��/�����ij���ʱ��Ϊ����Сʱ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������y=kx-2��k��0����ͼ������һ���ޣ���ô����y= ![]() ��ͼ��һ���ڣ���������
��ͼ��һ���ڣ���������
A.��һ��������
B.������������
C.��һ��������
D.�ڶ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����y=-x2+4x-2����y=a(x+m)2+n����ʽ��m,n��ֵ�ֱ��ǣ� ��
A.m=-2,n=-2B.m=-2,n=-6C.m=2,n=-2D.m=-2,n=2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ȫ�ȵ�ֱ���������ص���һ�𣬽����е�һ�����������ŵ�B��C�ķ���ƽ�Ƶ���DEF��λ�ã�AB=10��DO=4��ƽ�ƾ���Ϊ6������Ӱ�������Ϊ�� �� 
A.24
B.40
C.42
D.48
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��G��������ABCD�Խ���AC��һ�㣬��GE��AD��GF��AB������ֱ�Ϊ��E��F.
��֤���ı���AFGE���ı���ABCD���ƣ�
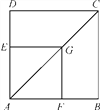
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y ����2��x��3��2��4�Ķ��������ǣ� ��
A.��3��4��B.��4��3��C.����3��4��D.��4����3��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com