
【题目】(本小题满分8分)某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体实验.测得成人服药后血液中药物深度![]() (微克/毫升)与服药时间
(微克/毫升)与服药时间![]() 小时之间的函数关系如图所示(当
小时之间的函数关系如图所示(当![]() 时,
时,![]() 与
与![]() 成反比).
成反比).

(1)根据图象分别求出血液中药物浓度上升和下降阶段![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)问血液中药物浓度不低于4微克/毫升的持续时间为多少小时?
【答案】(1)血液中药物浓度上升时![]() ;血液中药物浓度下降时,
;血液中药物浓度下降时,![]() .
.
(2)血液中药物浓度不低于4微克/毫升持续时间为6小时.
【解析】
试题分析:(1)根据图象利用待定系数法,抓住关键点(4,8)分别求出血液中药物浓度上升和下降阶段![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)可以令y=4也可以根据题意列不等式,现血液中药物浓度不低于4微克/毫升即:![]() ,解不等式组即可.
,解不等式组即可.
试题解析:解:(1)由图象可知,当![]() 时,
时,![]() 与
与![]() 成正比例关系,设
成正比例关系,设![]() .
.
由图象可知,当![]() 时,
时,![]() ,∴
,∴![]() ,解得:
,解得:![]() ;
;
∴![]()
又由题意可知:当![]() 时,
时,![]() 与
与![]() 成反比,设
成反比,设![]() .
.
由图象可知,当![]() 时,
时,![]() ,∴
,∴![]() ;
;
∴![]()
即:血液中药物浓度上升时![]() ;血液中药物浓度下降下
;血液中药物浓度下降下![]() .
.
(2)血液中药物浓度不低于4微克/毫升即:![]()
∴![]() 且
且![]() ,解得
,解得![]() 且
且![]() ;
;
∴![]() ,即持续时间为6小时.
,即持续时间为6小时.


 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
【题目】下列计算错误的是( )
A. (6a+1)(6a﹣1)=36a2﹣1 B. (a3﹣8)(﹣a3+8)=a9﹣64
C. (﹣m﹣n)(m﹣n)=n2﹣m2 D. (﹣a2+1)(﹣a2﹣1)=a4﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
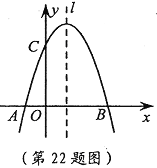
【题目】(本题10分)如图,已知抛物线![]() 与
与![]() 轴交于A,B两点,与
轴交于A,B两点,与![]() 轴交于点C,点B的坐标为(3,0)。
轴交于点C,点B的坐标为(3,0)。
(1)求m的值及抛物线的顶点坐标;
(2)点P是抛物线对称轴![]() 上的一个动点,当PA+PC的值最小时,求点P的坐标。
上的一个动点,当PA+PC的值最小时,求点P的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应“低碳生活”的号召,李明决定每天骑自行车上学,有一天李明骑了1000米后,自行车发生了故障,修车耽误了5分钟,车修好后李明继续骑行,用了8分钟骑行了剩余的800米,到达学校(假设在骑车过程中匀速行驶).若设他从家开始去学校的时间为t(分钟),离家的路程为y(千米),则y与t(15<t≤23)的函数关系为( )
A.y=100t(15<t≤23)
B.y=100t-500(15<t≤23)
C.y=50t+650(15<t≤23)
D.y=100t+500(15<t≤23)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com