【题目】如图，CB切⊙O于点B，CA交⊙O于点D且AB为⊙O的直径，点E是 
上异于点A、D的一点．若∠C=40°，则∠E的度数为 ． 
科目：初中数学 来源： 题型：
【题目】在数学课上，老师提出如下问题：如何使用尺规完成“过直线l外一点A作已知直线l的平行线”．
小云的作法如下：
（1）在直线l 上任取一点B，以点B为圆心，AB长为半径作弧， 交直线l 于点C；
（2）分别以A，C为圆心，以AB长为半径作弧，两弧相交于点D；
（3）作直线AD．
所以直线AD即为所求．
老师说：“小云的作法正确”．
请回答：小云的作图依据是____________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】点A在数轴上对应的数为a，点B对应的数为b，且a，b满足：|a＋3|＋(b－2)2=0
（1）求线段AB的长；
（2）如图①，点C在数轴上对应的数为x，且是方程
的根，在数轴上是否存在点M使MA＋MB＝
BC＋AB？若存在，求出点M对应的数；若不存在，说明理由；
（3）如图②，若N点是B点右侧一点，NA的中点为Q，P为NB的三等分点且靠近于B点，当N在B的右侧运动时，请直接判断
的值是不变的还是变的，如果不变请直接写出其值，如果是变的请说明理由．
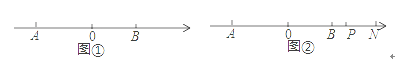
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将△ABC纸片沿DE折叠，使点A落在点A'处，且A'B平分∠ABC，A'C平分∠ACB，若∠BA'C=110°，则∠1+∠2的度数为（ ）
A. 80°； B. 90°； C. 100°； D. 110°；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知△ABC的周长是20，三边分别为a，b，c.
(1)若b是最大边，求b的取值范围；
(2)若△ABC是三边均不相等的三角形，b是最大边，c是最小边，且b＝3c，a，b，c均为整数，求△ABC的三边长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，O为直线AB上一点，∠AOC＝50°，OD平分∠AOC，∠DOE＝90°.
(1)请你数一数，图中有多少个小于平角的角；
(2)求出∠BOD的度数；
(3)请通过计算说明OE是否平分∠BOC.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，I点为△ABC的内心，D点在BC上，且ID⊥BC，若∠B=44°，∠C=56°，则∠AID的度数为何？（ ）
A. 174 B. 176 C. 178 D. 180
查看答案和解析>>
科目：初中数学 来源： 题型：
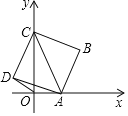
【题目】如图，点A是x轴上的一个动点，点C在y轴上，以AC为对角线画正方形ABCD，已知点C的坐标是
，设点A的坐标为
．
当
时，正方形ABCD的边长
______．
连结OD，当
时，
______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在篮球比赛中，某队员连续10场比赛中每场的得分情况如下所示：
场次（场） | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
得分（分） | 13 | 4 | 13 | 16 | 6 | 19 | 4 | 4 | 7 | 18 |
则这10场比赛中该队员得分的中位数和众数分别是（ ）
A.10，4
B.10，13
C.11，4
D.12.5，13
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
