
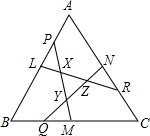
 正△ABC,在边AB、BC、CA的正中间分别取点L、M、N,在边AL、BM、CN上分别取点P、Q、R,使LP=MQ=NR,当PM和RL、PM和QN、QN和RL的相交点分别是X、Y、Z时,使XY=XL,这时,△XYZ的面积是△ABC的几分之几?请写出思考过程.
正△ABC,在边AB、BC、CA的正中间分别取点L、M、N,在边AL、BM、CN上分别取点P、Q、R,使LP=MQ=NR,当PM和RL、PM和QN、QN和RL的相交点分别是X、Y、Z时,使XY=XL,这时,△XYZ的面积是△ABC的几分之几?请写出思考过程. 分析 根据对称性确定△XYZ是等边三角形,设出△XYZ的面积,证明△NYM的面积为△XYZ的面积的2倍,表示出△ABC的面积,得到答案.
解答 答:△XYZ的面积是△ABC的面积的$\frac{1}{28}$.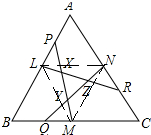 证明:连接LM、MN、LN,
证明:连接LM、MN、LN,
∵BP=CQ=AR,∠A=∠B=∠C,BM=CN=AL,
∴△PBM≌△QCN≌△RAL,
∴∠BPM=∠CQN=∠ARL,
根据对称性可知,△XYZ是等边三角形,
又∵LP=MQ=NR,
∴△XPL≌△YQN≌△ZRN,
LX=YM=ZN=XY=XZ=YZ
设△XYZ的面积为a,
∵Z是YN的中点,
∴N到PM的距离为Z到PM的距离的2倍,
∴△NYM的面积为2a,
∵△PLM≌△QMN≌△RNL,
∴△XLM≌△YMN≌△ZNL,
∴△MNL的面积为7a,
△ABC的面积为28a,
∴△XYZ的面积是△ABC的面积的$\frac{1}{28}$.
点评 本题考查的是等边三角形的性质和三角形确定的判定和性质,设出△XYZ的面积,通过三角形确定和面积公式得到△ABC的面积是解题的关键,解答本题时,要求学生具有较强的逻辑思维能力和推理能力.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
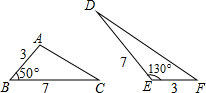 如图,若△ABC和△DEF的面积分别为S1,S2,则( )
如图,若△ABC和△DEF的面积分别为S1,S2,则( )| A. | S1=$\frac{1}{2}$S2 | B. | S1=$\frac{7}{2}$S2 | C. | S1=$\frac{8}{5}$S2 | D. | S1=S2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 170 | B. | 176 | C. | 178 | D. | 183 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com