
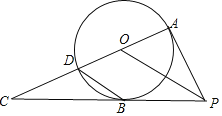
【题目】如图,PA是⊙O的切线,A为切点.B为⊙O上一点,连接AO并延长,交⊙O于点D.交PB的延长线于点C连接PO,若PA=PB.
(1)求证:PB是⊙O的切线;
(2)连接DB,若∠C=30°,求证:D是CO的中点.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
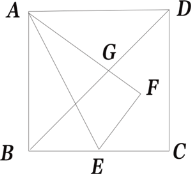
【题目】如图,已知正方形ABCD的边长为6,E为BC的中点,将△ABE沿直线AE折叠后,点B落在点F处,AF交对角线BD于点G,则FG的长是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴的一个交点为
轴的一个交点为![]() ,与
,与![]() 轴的交点
轴的交点![]() 在点
在点![]() 与点
与点![]() 之间(包含端点),顶点
之间(包含端点),顶点![]() 的坐标为
的坐标为![]() 。则下列结论:①
。则下列结论:①![]() ;②
;②![]() ;③对于任意实数
;③对于任意实数![]() ,
,![]() 总成立;④关于
总成立;④关于![]() 的方程
的方程![]() 没有实数根。其中结论正确的个数为()
没有实数根。其中结论正确的个数为()

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=﹣![]() x2+
x2+![]() x+
x+![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D.

(1)求直线BC的解析式;
(2)如图2,点P为直线BC上方抛物线上一点,连接PB、PC.当△PBC的面积最大时,在线段BC上找一点E(不与B、C重合),使PE+![]() BE的值最小,求点P的坐标和PE+
BE的值最小,求点P的坐标和PE+![]() BE的最小值;
BE的最小值;
(3)如图3,点G是线段CB的中点,将抛物线y=﹣![]() x2+
x2+![]() x+
x+![]() 沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为F.在抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为直角三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为F.在抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为直角三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生准备购买标价为50元的《现代汉语词典》,现有甲、乙两书店出售此书,甲店按如下方法促销:若只购1本,则按原价销售;若一次性购买多于1本,但不多于30本时,每多购一本,售价在标价的基础上优惠2%(例如买2本,每本售价优惠2%;买三本,每本售价优惠4%,以此类推);若多于30本,每本售价20元.乙书店一律按标价的6折销售.
(1)分别写出在两书店购买此书总价y甲、y乙与购书本数x之间的函数关系式;
(2)若这些学生一次性购买多于30本时,那么去哪家书店购买更划算,为什么?若要一次性购买不多于30本时,先写出y(y=y甲﹣y乙)与购买本数x之间的函数式,画出其图象,再利用函数图象分析去哪家书店购买更划算.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲、乙两个不透明的布袋里,都装有3个大小、材质完全相同的小球,其中甲袋中的小球上分别标有数字0,1,2;乙袋中的小球上分别标有数字﹣1,﹣2,0.现从甲袋中任意摸出一个小球,记其标有的数字为x,再从乙袋中任意摸出一个小球,记其标有的数字为y,以此确定点M的坐标(x,y).
(1)请你用画树状图或列表的方法,写出点M所有可能的坐标;
(2)求点M(x,y)在函数y=﹣![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班数学兴趣小组对函数![]() 的图象和性质进行了探究,探究过程如下,请补充完整:
的图象和性质进行了探究,探究过程如下,请补充完整:
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数, ![]() 与
与![]() 的几组对应值如下:
的几组对应值如下:
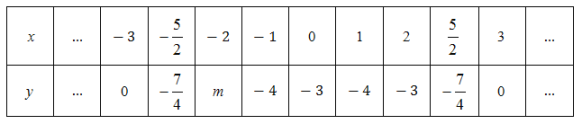
其中,![]() ________.
________.
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
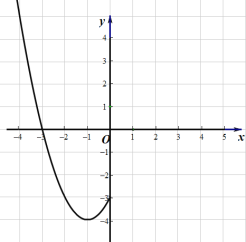
(3)观察函数![]() 图象,回答下列问题:
图象,回答下列问题:
①函数图像的对称性是: .
②当![]() 时,写出
时,写出![]() 随
随![]() 的变化规律: .
的变化规律: .
(4)进一步探究函数图象发现:方程![]() 有________个实数根.
有________个实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法,正确的是( )
A.某事件发生的概率为![]() ,就是说,在两次重复的试验中,必有一次发生
,就是说,在两次重复的试验中,必有一次发生
B.一不透明袋子里有100个球,小明摸了8次,每次都只摸到黑球,没摸到白球,因此小明断定:袋子里面只有黑球,没有白球
C.将两枚一元硬币同时抛下,可能出现的情形有:(1)两枚均为正;(2)两枚均为反;(3)一正一反;所以同时抛掷两枚硬币,出现一正一反的概率是![]()
D.八年级共有400名同学,一定会有人同一天过生日
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】马路两侧有两根灯杆AB、CD,当小明站在点N处时,在灯C的照射下小明的影长正好为NB,在灯A的照射下小明的影长为NE,测得BD=24m,NB=6m,NE=2m.
(1)若小明的身高MN=1.6m,求AB的长;
(2)试判断这两根灯杆的高度是否相等,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com