
【题目】如图,抛物线![]() 与
与![]() 轴的一个交点为
轴的一个交点为![]() ,与
,与![]() 轴的交点
轴的交点![]() 在点
在点![]() 与点
与点![]() 之间(包含端点),顶点
之间(包含端点),顶点![]() 的坐标为
的坐标为![]() 。则下列结论:①
。则下列结论:①![]() ;②
;②![]() ;③对于任意实数
;③对于任意实数![]() ,
,![]() 总成立;④关于
总成立;④关于![]() 的方程
的方程![]() 没有实数根。其中结论正确的个数为()
没有实数根。其中结论正确的个数为()

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
【答案】B
【解析】
利用抛物线的对称轴方程得到b=-2a,再利用x=-1时,a-b+c=0,则3a+c=0,于是可对①进行判断;由于-3≤c≤-2,c=-3a,所以-3≤-3a≤-2,解不等式组可对②进行判断;利用x=1时,二次函数有最小值n,则可对③进行判断;利用直线y=n与y=ax2+bx+c只有一个公共点,则直线y=n+1与y=ax2+bx+c有两个公共点,于是可对④进行判断.
∵抛物线的对称轴为直线x=-![]() =1,
=1,
∴b=-2a,
∵x=-1时,y=0,
即a-b+c=0,
∴a+2a+c=0,即3a+c=0,所以①正确;
∵抛物线与y轴的交点B在点(0,-2)与点(0,-3)之间(包含端点),
∴-3≤c≤-2,
而c=-3a,
∴-3≤-3a≤-2,
∴![]() ≤a≤1,所以②错误;
≤a≤1,所以②错误;
∵顶点D的坐标为(1,n).抛物线开口向上,
∴x=1时,二次函数有最小值n,
∴a+b+c≤am2+bm+c,
即对于任意实数m,a+b≤am2+bm总成立,所以③正确;
∵顶点D的坐标为(1,n).
∴直线y=n与y=ax2+bx+c只有一个公共点,
∴直线y=n+1与y=ax2+bx+c有两个公共点,
即关于x的方程ax2+bx+c=n+1有两个实数根,所以④错误.
故选:B.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
【题目】商场销售一批名牌衬衫,平均每天可售出40件,每件盈利40元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出4件.
(1)若商场平均每天要盈利2400元,每件衬衫应降价多少元?
(2)若该商场要每天盈利最大,每件衬衫应降价多少元?盈利最大是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ACB中,∠C=90°,AC=3,BC=4,O是BC的中点,到点O的距离等于![]() BC的所有点组成的图形记为G,图形G与AB交于点D.
BC的所有点组成的图形记为G,图形G与AB交于点D.

(1)补全图形并求线段AD的长;
(2)点E是线段AC上的一点,当点E在什么位置时,直线ED与 图形G有且只有一个交点?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
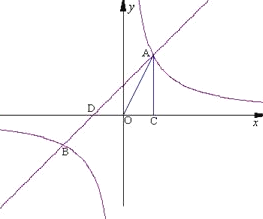
【题目】如图,已知反比例函数![]() (k1>0)与一次函数
(k1>0)与一次函数![]() 相交于A、B两点,AC⊥x轴于点C. 若△OAC的面积为1,且tan∠AOC=2 .
相交于A、B两点,AC⊥x轴于点C. 若△OAC的面积为1,且tan∠AOC=2 .
(1)求出反比例函数与一次函数的解析式;
(2)请直接写出B点的坐标,并指出当x为何值时,反比例函数y1的值大于一次函数y2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,AC与BD交于点E,点E是BD的中点,延长CD到点F,使DF=CD,连接AF,
(1)求证:AE=CE;
(2)求证:四边形ABDF是平行四边形;
(3)若AB=2,AF=4,∠F=30°,则四边形ABCF的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
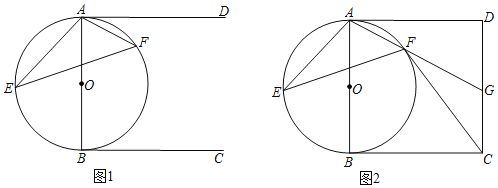
【题目】已知,AB是⊙O的直径,E、F是⊙O上的点,连接AE、AF、EF,BC是⊙O的切线,过点A作AD∥BC.
(1)如图1,求证:∠DAF=∠AEF;
(2)如图2,若AD=BC=AB,连接CD,延长AF交CD于G,连接CF,若FC=BC=4,求AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点都在方格线的交点(格点)上.
(1)将△ABC绕C点按逆时针方向旋转90°得到△A′B′C′,请在图中画出△A′B′C′.
(2)将△ABC向上平移1个单位,再向右平移5个单位得到△A″B″C″,请在图中画出△A″B″C″.
(3)若将△ABC绕原点O旋转180°,A的对应点A1的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
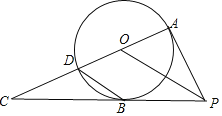
【题目】如图,PA是⊙O的切线,A为切点.B为⊙O上一点,连接AO并延长,交⊙O于点D.交PB的延长线于点C连接PO,若PA=PB.
(1)求证:PB是⊙O的切线;
(2)连接DB,若∠C=30°,求证:D是CO的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC看,∠BAC=90°,AC=12,AB=10,D是AC上一个动点,以AD为直径的⊙O交BD于E,则线段CE的最小值是( )

A. 5 B. 6 C. 7 D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com