
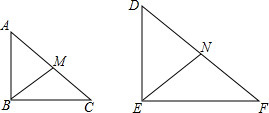
 如图,Rt△ABC∽Rt△DEF,且DE=2AB,BM,EN是斜边上的中线
如图,Rt△ABC∽Rt△DEF,且DE=2AB,BM,EN是斜边上的中线分析 (1)根据相似三角形的性质得到$\frac{BC}{EF}=\frac{AC}{DF}=\frac{BM}{EN}$,由直角三角形的性质得到CM=$\frac{1}{2}$AC,FN=$\frac{1}{2}$DF,于是得到$\frac{BC}{EF}=\frac{BM}{EN}=\frac{CM}{NF}$,即可得到结论;
(2)根据相似三角形的性质得到$\frac{AC}{DF}=\frac{AB}{DE}$=$\frac{1}{2}$,代入数据即可得到结论.
解答 解:(1)∵Rt△ABC∽Rt△DEF,BM,EN是斜边上的中线,
∴$\frac{BC}{EF}=\frac{AC}{DF}=\frac{BM}{EN}$,
∵CM=$\frac{1}{2}$AC,FN=$\frac{1}{2}$DF,
∴$\frac{BC}{EF}=\frac{BM}{EN}=\frac{CM}{NF}$,
∴△BMC∽△ENF;
(2)∵Rt△ABC∽Rt△DEF,
∴$\frac{AC}{DF}=\frac{AB}{DE}$=$\frac{1}{2}$,
∵AC=3,
∴DF=6,
∵EN是斜边上的中线
∴EN=$\frac{1}{2}$DF=3.
点评 本题考查了相似三角形的判定和性质,直角三角形的性质,熟练掌握相似三角形的判定和性质是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在直线CD上有一动点P,P在CD上从右往左运动的过程中,找出:
如图,在直线CD上有一动点P,P在CD上从右往左运动的过程中,找出:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次跳到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次再跳到点N关于点C的对称点K处…如此继续下去.
如图所示,在平面直角坐标系中,一颗棋子从点P处开始依次关于点A,B,C作循环对称跳动,即第一次跳到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次再跳到点N关于点C的对称点K处…如此继续下去.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
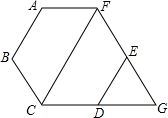 已知:如图,正六边形ABCDEF的边长为6cm.延长FE,CD相交于点G.
已知:如图,正六边形ABCDEF的边长为6cm.延长FE,CD相交于点G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com