
【题目】如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.
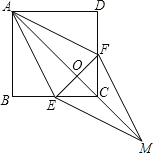
(1)求证:BE=DF
(2)连接AC交EF于点D,延长OC至点M,使OM=OA,连结EM、FM,试证明四边形AEMF是菱形.
【答案】(1)、证明过程见解析;(2)、证明过程见解析
【解析】
试题分析:(1)、根据正方形的性质可得AB=AD,∠B=∠D=90°,然后利用“HL”证明Rt△ABE和Rt△ADF全等,根据全等三角形对应边相等可得BE=DF;(2)、求出CE=CF,然后利用“边边边”证明△AEC和△AFC全等,根据全等三角形对应角相等可得∠EAC=∠FAC,再根据等腰三角形三线合一的性质可得AC垂直平分EF,根据线段垂直平分线上的点到两端点的距离相等可得EM=FM,再判断出EF垂直平分AM,根据线段垂直平分线上的点到两端点的距离相等可得AE=EM,然后根据四条边都相等的四边形是菱形证明.
试题解析:(1)、在正方形ABCD中,AB=AD,∠B=∠D=90°, 在Rt△ABE和Rt△ADF中,![]() ,
,
∴Rt△ABE≌Rt△ADF(HL), ∴BE=DF;
(2)、∵BC=CD,BE=DF, ∴BC﹣BE=CD﹣CF, 即CE=CF,
在△AEC和△AFC中,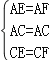 , ∴△AEC≌△AFC(SSS), ∴∠EAC=∠FAC,
, ∴△AEC≌△AFC(SSS), ∴∠EAC=∠FAC,
又∵AE=AF, ∴AC垂直平分EF, ∴EM=FM, ∵OM=OA, ∴EF垂直平分AM,
∴AE=EM, ∴AE=EM=FM=AF, ∴四边形AEMF是菱形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
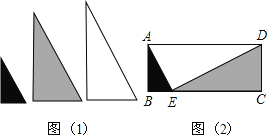
【题目】如图1,用形状相同、大小不等的三块直角三角形木板,恰好能拼成如图2所示的四边形ABCD,若AE=4,CE=3BE,那么这个四边形的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一元二次方程 4x2+5x=81 化成一般式后,如果二次项系数是 4,则一次项系数和常数项分别是( )
A. 5,81 B. 5,﹣81 C. ﹣5,81 D. 5x,﹣81
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有4个除颜色外完全相同的小球,其中黄球1个,红球1个,白球2个,“从中任意摸出2个球,它们的颜色相同”这一事件是事件.(填“随机”或者“确定”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个数用科学记数法表示出来是3.02×10﹣6 , 则原来的数应该是( )
A.0.00000302
B.0.000000302
C.3020000
D.302000000
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com