
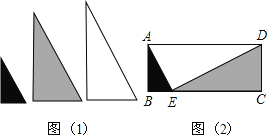
【题目】如图1,用形状相同、大小不等的三块直角三角形木板,恰好能拼成如图2所示的四边形ABCD,若AE=4,CE=3BE,那么这个四边形的面积是 .
【答案】16![]()
【解析】
试题分析:依题意可以得到△ABE∽△ECD∽△DEA,∠B=∠C=∠D=90°,利用相似三角形的性质可以推出BE:CD=AB:EC,而四边形ABCD为矩形,可以得到AB=CD,所以AB2=BEEC,又因为CE=3BE,可以得到AB=![]() BE,由此可以求出BE,CB,最后就可以求出面积.
BE,由此可以求出BE,CB,最后就可以求出面积.
∵形状相同、大小不等的三块直角三角形木板, ∴△ABE∽△ECD∽△DEA,∠B=∠C=∠AED=90°,
∴BE:CD=AB:EC, ∴四边形ABCD为矩形, ∴AB=CD, ∴![]() =BEEC,
=BEEC,
∵CE=3BE, ∴AB=![]() BE, ∵AE=4, ∴BE=2,AB=2
BE, ∵AE=4, ∴BE=2,AB=2![]() , ∴BC=BE+CE=4BE=8,
, ∴BC=BE+CE=4BE=8,
∴这个四边形的面积是S=AB×BC=2![]() ×8=16
×8=16![]() .
.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①b2>4ac;②abc>0;③2a﹣b=0;④8a+c<0;⑤9a+3b+c<0,其中结论正确有( )个。

A.2个 B.3个 C.4个 D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.
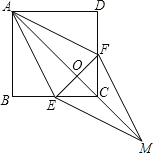
(1)求证:BE=DF
(2)连接AC交EF于点D,延长OC至点M,使OM=OA,连结EM、FM,试证明四边形AEMF是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com