练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在平面直角坐标系xOy中，矩形ABCD的AB边在x轴上，且AB=3，AD=2，经过点C的直线y=x-2与x轴、y轴分别交于点E、F．

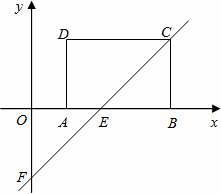    （1）求矩形ABCD的顶点A、B、C、D的坐标；

    （2）求证：△OEF≌△BEC；

    （3）P为直线y=x-2上一点，若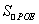=5，求点P的坐标．


    （1）点A、B、C、D的坐标分别为（1，0）、（4，0）、（4，2），（1，2）．

    （2）（2）直线y=x-2与x轴、y轴坐标分别为E （2，0）、F （0，-2），

    ∴OF=OE=BC=BE=2，在RT△OEF和RT△BEC中，

    ，故可得△OEF≌△BEC．

    （3）设点P的坐标为，则=×OE×=×2×=5，

    解得：=±5，

    ①当=5时，=7；②当=-5时，=-3，

    故点P的坐标为（7，5）或（-3，-5）．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，五边形ABCDE中，AB∥CD，∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC的外角，则∠1+∠2+∠3=__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某校校园超市老板到批发中心选购甲、乙两种品牌的文具盒，乙品牌的进货单价是甲品牌进货单价的2倍，考虑各种因素，预计购进乙品牌文具盒的数量y（个）与甲品牌文具盒的数量x（个）之间的函数关系如图所示．当购进的甲、乙品牌的文具盒中，甲有120个时，购进甲、乙品牌文具盒共需7200元．

    （1）根据图象，求y与x之间的函数关系式；

    （2）求甲、乙两种品牌的文具盒进货单价；

    （3）若该超市每销售1个甲种品牌的文具盒可获利4元，每销售1个乙种品牌的文具盒可获利9元，根据学生需求，超市老板决定，准备用不超过6300元购进甲、乙两种品牌的文具盒，且这两种品牌的文具盒全部售出后获利不低于1795元，问该超市有几种进货方案？哪种方案能使获利最大？最大获利为多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知直线与x轴的交点在A（2，0）、B（3，0）之间（包括A、B两点），则的取值范围是              ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知某正数的两个平方根分别是和，的立方根是-2，求的算术平方根.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列各数－5，，4.11212121212…，0，中，无理数有(    )

      A．1个        B．2个         C．3个     D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    按下面的程序计算：

      若输入x ＝100，输出结果是501，若输入x＝25，输出结果是631，若开始输入的x值为正整数，最后输出的结果为556，则开始输入的x值可能有(     )

        A．1种             B．2种              C．3种             D．4种

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若不等式ax<b的解集是x>，则a的取值范围是(    )

      A．a>0           B．a≤0      C．a>0       D．a<0

    查看答案和解析>>

    同步练习册答案