
【题目】如图,已知四边形ABCD和四边形DEFG为正方形,点E在线段DC上,点A,D,G在同一直线上,且AD=3,DE=1,连接AC,CG,AE,并延长AE交CG于点H.
(1)求sin∠EAC的值;
(2)求线段AH的长.

【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:
(1)如图,过点E作EM⊥AC于点M,则∠EMA=∠EMC=90°,△EMC为等腰直角三角形,在Rt△ADE中易得AE=![]() ,在Rt△EMC中易得EM=
,在Rt△EMC中易得EM=![]() ,∴sin∠EAM=
,∴sin∠EAM=![]() ;
;
(2)由已知易证△ADE≌△CDG,从而可得GC=AE=![]() ,∠DAE=∠DCG,由此可证得AH⊥CG,最后利用S△AGC=
,∠DAE=∠DCG,由此可证得AH⊥CG,最后利用S△AGC= ![]() 可解得AH的长.
可解得AH的长.
试题解析:
(1)作EM⊥AC于M.
∵四边形ABCD是正方形,
∴∠ADC=90°,AD=DC=3,∠DCA=45°.
在Rt△ADE中,∵∠ADE=90°,AD=3,DE=1,
∴AE=![]() .
.
在Rt△EMC中,∵∠EMC=90°,∠ECM=45°,EC=2,
∴EM=CM=![]() .
.
∴在Rt△AEM中,sin∠EAM=![]() ;
;

(2)在△GDC和△EDA中,  ,
,
∴△GDC≌△EDA,
∴∠GCD=∠EAD,GC=AE=![]() .
.
又∵∠AED=∠CEH,
∴∠EHC=∠EDA=90°,
∴AH⊥GC.
∵S△AGC=![]() AG·DC=
AG·DC=![]() GC·AH,
GC·AH,
∴![]() ×4×3=
×4×3=![]()
![]() ×AH,
×AH,
∴AH=![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 和双曲线
和双曲线![]() (k为正整数)交于A,B两点.
(k为正整数)交于A,B两点.
(1)当k=1时,求A、B两点的坐标;
(2)当k=2时,求△AOB的面积;
(3)当k=1时,△OAB的面积记为S1,当k=2时,△OAB的面积记为S2,…,依此类推,当k=n时,△OAB的面积记为Sn,若S1+S2+…+Sn=![]() ,求n的值.
,求n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①三角形的外角大于内角;②各条边都相等,各个角都相等的多边形是正多边形;③三角形的三条高相交于一点;④如果a>b,那么m2a>m2b,其中说法正确的有( ).
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,对角线AC、BD相交于点O,过点O与AD上的一点E作直线OE,交BA的延长线于点F.若AD=4,DC=3,AF=2,则AE的长是( )
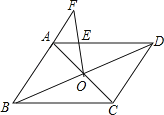
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下问题,不适合使用全面调查的是( )
A. 对旅客上飞机前的安检B. 航天飞机升空前的安全检查
C. 了解全班学生的体重D. 了解广州市中学生每周使用手机所用的时间
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com