
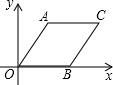
 ?AOBC如图放置,A(1,2),B(2,0),先将平行四边形向左平移6个单位长度,再向下平移1个单位长度,然后沿x轴翻折,最后绕坐标原点O旋转90°得到点C的对应点为点P,则点P的坐标为(-1,3)或(1,-3).
?AOBC如图放置,A(1,2),B(2,0),先将平行四边形向左平移6个单位长度,再向下平移1个单位长度,然后沿x轴翻折,最后绕坐标原点O旋转90°得到点C的对应点为点P,则点P的坐标为(-1,3)或(1,-3). 分析 根据菱形的对称性求出点B的坐标,再求出AB的中点的坐标,进而求出点C的坐标,根据向左平移横坐标减,向下平移纵坐标减求出平移后的C点对应的坐标,结合翻折变换知识求出沿x轴翻折后C点对应的坐标,再根据旋转的性质确定点P的坐标.
解答 解:∵A(1,2),B(2,0),
∴点C坐标为(3,2),
∵向左平移6个单位长度,再向下平移1个单位长度,
∴3-6=-3,2-1=1,
∴平移后点C对应的坐标为(-3,1),
沿x轴翻折后C点对应的坐标为(-3,-1),
∵在坐标平面内绕点O旋转90°,
∴若是顺时针旋转,则对应点在第二象限,坐标为(-1,3),
若是逆时针旋转,则对应点在第四象限,坐标为(1,-3),
综上所述,点P的坐标为(-1,3)或(1,-3),
故答案为(-1,3)或(1,-3).
点评 本题考查了菱形的性质,坐标与图形的变化,熟练掌握菱形的性质以及平移、旋转变换的性质是解题的关键.


科目:初中数学 来源: 题型:解答题
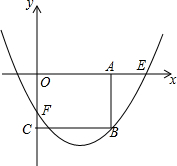 如图,在平面直角坐标系中,抛物线y=$\frac{1}{a}{x}^{2}-\frac{4}{a}x-a$(a>0)与x轴正半轴交于点E,与y轴交于点F,过点A(2a,0)作AB∥y轴,交抛物线于点B,过点B作BC⊥y轴于点C.
如图,在平面直角坐标系中,抛物线y=$\frac{1}{a}{x}^{2}-\frac{4}{a}x-a$(a>0)与x轴正半轴交于点E,与y轴交于点F,过点A(2a,0)作AB∥y轴,交抛物线于点B,过点B作BC⊥y轴于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 5 | D. | 以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省句容市华阳片八年级下学期第一次月考数学试卷(解析版) 题型:填空题
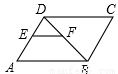
如图,在?ABCD中,BD为对角线,E、F分别是AD、BD的中点,连接 EF.若EF=3,则CD的长为 .
查看答案和解析>>
科目:初中数学 来源:2017届陕西省宝鸡市渭滨区九年级上学期期末考试数学试卷(解析版) 题型:填空题
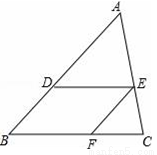
如图,在△ABC中,点D,E,F分别在AB,AC,BC上,DE∥BC,EF∥AB.若AB=8,BD=3,BF=4,则FC的长为 .
查看答案和解析>>
科目:初中数学 来源:2017届云南省普洱市九年级学业水平测试模拟考试(一)数学试卷(解析版) 题型:判断题
如图,直线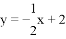 与
与 轴交于点B,与
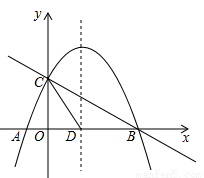
轴交于点B,与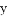 轴交于点C,已知二次函数的图象经过点B、C和点A(-1,0).
轴交于点C,已知二次函数的图象经过点B、C和点A(-1,0).
(1)求该二次函数的关系式;
(2)若抛物线的对称轴与 轴的交点为点D,则在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
轴的交点为点D,则在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com