
分析 (1)根据题意写出一个分母中有未知数的不等式即可;
(2)类比以上作法分x-3>0、x-3<0两种情况,分别去分母得到两个不等式组,解不等式组可得;
(3)观察到不等式分母x2+2x+1=(x+1)2≥0,直接去分母可得不等式,解不等式可得解集.
解答 解:(1)$\frac{2x}{x-2}<1$;
(2)当x-3>0时,去分母,得:3x+2≥x-3;
当x-3<0时,去分母,得:3x+2≤x-3;
∴$\left\{\begin{array}{l}{x-3>0}\\{3x+2≥x-3}\end{array}\right.$或$\left\{\begin{array}{l}{x-3<0}\\{3x+2≤x-3}\end{array}\right.$,
分别解不等式组,得:x>3或x≤-5,
所以原不等式的解集为:x>3或x≤-5;
(3)∵x2+2x+1=(x+1)2≥0,
∴去分母,得:-2x2+3x<-2(x2+2x+1),
解得:x<-$\frac{2}{7}$,
又(x+1)2≠0,即x≠-1,
∴原不等式的解集为:x<-$\frac{2}{7}$且x≠-1.
点评 本题主要考查解分式不等式的能力和类比的作法,熟知不等式的基本性质是解题的根本,理解和掌握例题的作法是解题的关键.


 教学练新同步练习系列答案
教学练新同步练习系列答案科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=-1}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-2}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-2}\\{y=-1}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
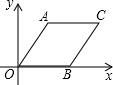 ?AOBC如图放置,A(1,2),B(2,0),先将平行四边形向左平移6个单位长度,再向下平移1个单位长度,然后沿x轴翻折,最后绕坐标原点O旋转90°得到点C的对应点为点P,则点P的坐标为(-1,3)或(1,-3).
?AOBC如图放置,A(1,2),B(2,0),先将平行四边形向左平移6个单位长度,再向下平移1个单位长度,然后沿x轴翻折,最后绕坐标原点O旋转90°得到点C的对应点为点P,则点P的坐标为(-1,3)或(1,-3).查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省句容市华阳片八年级下学期第一次月考数学试卷(解析版) 题型:填空题
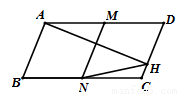
如图,在平行四边形ABCD中,AD=2AB,AH⊥CD于H,M为AD的中点,MN∥AB,连接NH,如果∠D=68°,则∠CHN=_______.
查看答案和解析>>
科目:初中数学 来源:2017届陕西省宝鸡市渭滨区九年级上学期期末考试数学试卷(解析版) 题型:判断题
(6分)某种商品的标价为400元/件,经过两次降价后的价格为324元/件,并且两次降价的百分率相同.
(1)求该种商品每次降价的百分率;
(2)若该种商品进价为300元/件,两次降价共售出此种商品100件,为使两次降价销售的总利润不少于3210元.问第一次降价后至少要售出该种商品多少件?
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省扬州市七年级下学期第一次月考数学试卷(解析版) 题型:单选题
如图,下列推理正确的是( )
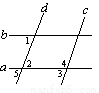
A. ∵∠1=∠3,∴ ∥
∥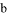 B. ∵∠1=∠2,∴
B. ∵∠1=∠2,∴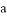 ∥
∥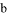
C. ∵∠1=∠2,∴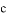 ∥
∥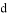 D. ∵∠1=∠3,∴
D. ∵∠1=∠3,∴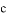 ∥
∥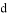
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com