
分析 (1)先把各二次根式化为最简二次根式,再计算小括号里面的运算,再相减即可求解;
(2)先把各二次根式化为最简二次根式,再去小括号,再合并计算即可求解.
解答 解:(1)($\sqrt{\frac{1}{8}}$-$\sqrt{32}$)-($\frac{1}{\sqrt{2}}$+2$\sqrt{\frac{1}{2}}$)
=($\frac{1}{4}$$\sqrt{2}$-4$\sqrt{2}$)-($\frac{1}{2}$$\sqrt{2}$+$\sqrt{2}$)
=-$\frac{15}{4}$$\sqrt{2}$-$\frac{3}{2}$$\sqrt{2}$
=-$\frac{21}{4}$$\sqrt{2}$;
(2)($\frac{9}{\sqrt{27}}$-$\sqrt{18}$)-(4$\sqrt{\frac{1}{2}}$-$\sqrt{12}$)
=($\sqrt{3}$-3$\sqrt{2}$)-(2$\sqrt{2}$-2$\sqrt{3}$)
=$\sqrt{3}$-3$\sqrt{2}$-2$\sqrt{2}$+2$\sqrt{3}$
=3$\sqrt{3}$-5$\sqrt{2}$.
点评 本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届陕西省宝鸡市渭滨区九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1使得BB1∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
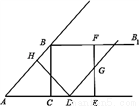
(1)当t为何值时,AD=AB,并求出此时DE的长度;
(2)当△DEG与△ACB相似时,求t的值.
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省扬州市七年级下学期第一次月考数学试卷(解析版) 题型:填空题
△ABC中,D为BC边上的一点,BD:BC=2:3,△ABC的面积为12,则△ABD的面积是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com