
【题目】如图,将平行四边形ABCD沿对角线BD进行折叠,折叠后点C落在点F处,DF交AB于点E.
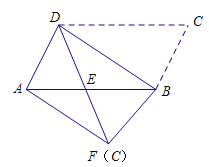
(1)求证:![]() ;
;
(2)判断AF与BD是否平行,并说明理由.
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据折叠的性质可证∠CDB =∠EDB,由平行四边形的性质,可证∠CDB =∠EBD,等量代换可证得结论;
(2)根据(1)结论可知DE=BE,然后由平行四边形的对边相等和等量代换,可知AE=EF,从而根据等边对等角可得∠EAF=∠EFA,再由三角形的内角和得出∠EDB= ∠EFA,因此可证得AF∥BD(或由AB与BD互相平分证得四边形ADBF是平行四边形).
(1)由折叠可知:∠CDB =∠EDB
∵四边形ABCD是平行四边形
∴DC∥AB
∴∠CDB =∠EBD
∴∠EDB=∠EBD
(2)∵∠EDB=∠EBD
∴DE=BE
由折叠可知:DC=DF
∵四边形ABCD是平行四边形
∴DC=AB
∴AE=EF
∴∠EAF=∠EFA
△BED中,∠EDB+∠EBD+∠DEB=180°
即2∠EDB+∠DEB=180°
同理△AEF中,2∠EFA+∠AEF=180°
∵∠DEB=∠AEF
∴∠EDB= ∠EFA
∴AF∥BD


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
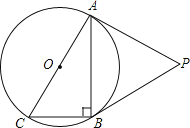
【题目】如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是⊙O外一点,PA切⊙O于点A,且PA=PB.
(1)求证:PB是⊙O的切线;
(2)已知PA=2![]() ,BC=2.求⊙O的半径.
,BC=2.求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验中学附近某水果超市最近新进了一批火龙果,每斤8元,为了合理定价,在第一周试行机动价格,卖出时每斤以10元为标准,超出10元的部分记为正,不足10元的部分记为负,超市记录第一周火龙果的售价情况和售出情况:
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
每斤相对于标准价格(元) | +1 | -2 | +3 | -1 | +2 | +5 | -4 |
售出斤数 | 20 | 35 | 10 | 30 | 15 | 5 | 50 |
(1)这一周超市售出的火龙果单价最高的是星期 , 最高单价是 元.
(2)这一周超市总共售出火龙果多少斤?总共卖得多少元钱?
(3)这一周超市出售此种火龙果的收益如何?(盈利或亏损的钱数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲、乙两地相距160km,![]() 、
、![]() 两车分别从甲、乙两地同时出发,
两车分别从甲、乙两地同时出发,![]() 车速度为85km/h,
车速度为85km/h,![]() 车速度为65km/h.
车速度为65km/h.
(1)![]() 、
、![]() 两车同时同向而行,
两车同时同向而行,![]() 车在后,经过几小时
车在后,经过几小时![]() 车追上
车追上![]() 车?
车?
(2)![]() 、
、![]() 两车同时相向而行,经过几小时两车相距20km?
两车同时相向而行,经过几小时两车相距20km?
查看答案和解析>>
科目:初中数学 来源: 题型:
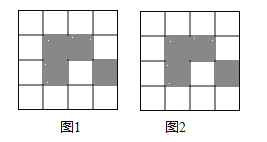
【题目】如图,下列4×4网格图都是由16个相同小正方形组成,每个网格图中有4个小正方形已涂上阴影,请在空白小正方形中,按下列要求涂上阴影.
(1)在图1中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个中心对称图形;
(2)在图2中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个轴对称图形,但不是中心对称图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
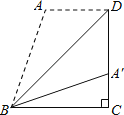
【题目】如图,梯形ABCD中,AD∥BC,DC⊥BC,将梯形沿对角线BD折叠,点A恰好落在DC边上的点A′处,若∠A′BC=20°,则∠A′BD的度数为_____°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知长方形ABCD中,AD=6cm,AB=4cm,点E为AD的中点.若点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BC上由点B向点C运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△AEP与△BPQ是否全等,请说明理由,并判断此时线段PE和线段PQ的位置关系;
(2)若点Q的运动速度与点P的运动速度相等,运动时间为t秒,设△PEQ的面积为Scm2,请用t的代数式表示S;
(3)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△AEP与△BPQ全等?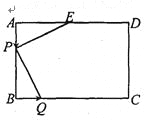
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等边三角形ABC中,CD为中线,点Q在线段CD上运动,将线段QA绕点Q顺时针旋转,使得点A的对应点E落在射线BC上,连接BQ,设∠DAQ=α
(0°<α<60°且α≠30°).
(1)当0°<α<30°时,
①在图1中依题意画出图形,并求∠BQE(用含α的式子表示);
②探究线段CE,AC,CQ之间的数量关系,并加以证明;
(2)当30°<α<60°时,直接写出线段CE,AC,CQ之间的数量关系.


![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com