
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§‘ΎΒ»±Ώ»ΐΫ«–ΈABC÷–Θ§CDΈΣ÷–œΏΘ§ΒψQ‘ΎœΏΕΈCD…œ‘ΥΕ·Θ§ΫΪœΏΕΈQA»ΤΒψQΥ≥ ±’κ–ΐΉΣΘ§ ΙΒΟΒψAΒΡΕ‘”ΠΒψE¬δ‘Ύ…δœΏBC…œΘ§Ν§Ϋ”BQΘ§…ηΓœDAQ=ΠΝ
Θ®0ΓψΘΦΠΝΘΦ60Γψ«“ΠΝΓΌ30ΓψΘ©.
Θ®1Θ©Β±0ΓψΘΦΠΝΘΦ30Γψ ±Θ§
ΔΌ‘ΎΆΦ1÷–“άΧβ“βΜ≠≥ωΆΦ–ΈΘ§≤Δ«σΓœBQEΘ®”ΟΚ§ΠΝΒΡ ΫΉ”±μ ΨΘ©ΘΜ
ΔΎΧΫΨΩœΏΕΈCEΘ§ACΘ§CQ÷°ΦδΒΡ ΐΝΩΙΊœΒΘ§≤ΔΦ”“‘÷ΛΟςΘΜ
Θ®2Θ©Β±30ΓψΘΦΠΝΘΦ60Γψ ±Θ§÷±Ϋ”–¥≥ωœΏΕΈCEΘ§ACΘ§CQ÷°ΦδΒΡ ΐΝΩΙΊœΒ.


![]()
ΓΨ¥πΑΗΓΩΘ®1Θ©ΔΌ![]() ΘΜΔΎCE+ACΘΫ
ΘΜΔΎCE+ACΘΫ![]() ΘΜΘ®2Θ©CEΘ≠ACΘΫ
ΘΜΘ®2Θ©CEΘ≠ACΘΫ![]() Θ§άμ”…ΦϊΫβΈω
Θ§άμ”…ΦϊΫβΈω
ΓΨΫβΈωΓΩ(1) ΔΌΗυΨί–ΐΉΣΒΡ–‘÷ ΦΑΒ»±Ώ»ΐΫ«–ΈΒΡΕ‘≥Τ–‘Ω…ΒΟQA=QBΘ§‘Ό”…QB=QEΩ…ΒΟ![]() ΘΜΔΎ―”≥ΛCAΒΫΒψFΘ§ ΙΒΟAF=CEΘ§Ν§Ϋ”QFΘ§ΉςQHΓΆAC”ΎΒψHΘ§
ΘΜΔΎ―”≥ΛCAΒΫΒψFΘ§ ΙΒΟAF=CEΘ§Ν§Ϋ”QFΘ§ΉςQHΓΆAC”ΎΒψHΘ§
Θ®1Θ©Β±0ΓψΘΦΠΝΘΦ30Γψ ±Θ§”…ΓœBQE=60Γψ+2ΠΝΩ…ΒΟΓœQEC=120Γψ+ΠΝΘ§‘Όάϊ”ΟΓςQAFΓ’ΓςQECΩ…ΒΟQF=QCΘ§”…Β»―ϋ»ΐΫ«–Έ»ΐœΏΚœ“ΜΒΡ–‘÷ Ω…ΒΟΓœACQ =30ΓψΘ§ΒΟΒΫΓςQCFΈΣΒ»―ϋ»ΐΫ«–ΈΘ§‘Όάϊ”ΟΫβ÷±Ϋ«»ΐΫ«–ΈΦ¥Ω…ΒΟ≥ωΫαΙϊ;(2)”…–ΐΉΣΒΡ–‘÷ Ω…ΒΟœΏΕΈCEΘ§ACΘ§CQ÷°ΦδΒΡ ΐΝΩΙΊœΒ.
ΔΌΜ≠≥ωΒΡΆΦ–Έ»γΆΦ9Υυ ΨΘ°
![]()
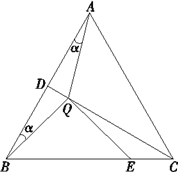
ΓΏ ΓςABCΈΣΒ»±Ώ»ΐΫ«–ΈΘ§
Γύ ΓœABC=60ΓψΘ°
ΓΏ CDΈΣΒ»±Ώ»ΐΫ«–ΈΒΡ÷–œΏΘ§
QΈΣœΏΕΈCD…œΒΡΒψΘ§
”…Β»±Ώ»ΐΫ«–ΈΒΡΕ‘≥Τ–‘ΒΟQA=QBΘ°
ΓΏ ΓœDAQ=ΠΝΘ§
Γύ ΓœABQ=ΓœDAQ=ΠΝΘ§ΓœQBE=60Γψ-ΠΝΘ°
ΓΏ œΏΕΈQEΈΣœΏΕΈQA»ΤΒψQΥ≥ ±’κ–ΐΉΣΥυΒΟΘ§
Γύ QE = QAΘ°
Γύ QB=QEΘ°
Ω…ΒΟ ![]()
![]() Θ°
Θ°
ΔΎ![]() Θ°
Θ°
÷ΛΖ®“ΜΘΚ»γΆΦ10Θ§―”≥ΛCAΒΫΒψFΘ§ ΙΒΟAF=CEΘ§Ν§Ϋ”QFΘ§ΉςQHΓΆAC”ΎΒψHΘ°
ΓΏ ΓœBQE=60Γψ+2ΠΝΘ§ΒψE‘ΎBC…œΘ§
Γύ ΓœQEC=ΓœBQE+ΓœQBE =(60Γψ+2ΠΝ)+( 60Γψ-ΠΝ)=120Γψ+ΠΝΘ°
ΓΏ ΒψF‘ΎCAΒΡ―”≥ΛœΏ…œΘ§ΓœDAQ=ΠΝΘ§

![]()
Γύ ΓœQAF=ΓœBAF+ΓœDAQ=120Γψ+ΠΝΘ°
Γύ ΓœQAF=ΓœQECΘ°
”÷ΓΏ AF =CEΘ§QA=QEΘ§
Γύ ΓςQAFΓ’ΓςQECΘ°
Γύ QF=QCΘ°
ΓΏ QHΓΆAC”ΎΒψHΘ§
Γύ FH=CHΘ§CF=2CHΘ°
ΓΏ ‘ΎΒ»±Ώ»ΐΫ«–ΈABC÷–Θ§CDΈΣ÷–œΏΘ§
ΒψQ‘ΎCD…œΘ§
Γύ ΓœACQ=![]() =30ΓψΘ§
=30ΓψΘ§
Φ¥ΓςQCFΈΣΒΉΫ«ΈΣ30ΓψΒΡΒ»―ϋ»ΐΫ«–ΈΘ°
Γύ ![]() Θ°
Θ°
Γύ ![]()
![]() Θ°
Θ°
Φ¥![]() Θ°
Θ°
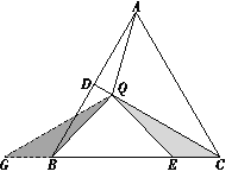
ΥΦ¬ΖΕΰΘΚ»γΆΦ11Θ§―”≥ΛCBΒΫΒψGΘ§ ΙΒΟBG=CEΘ§Ν§Ϋ”QGΘ§Ω…ΒΟ
ΓςQBGΓ’ΓςQECΘ§ΓςQCGΈΣΒΉΫ«ΈΣ30ΓψΒΡΒ»―ϋ»ΐΫ«–ΈΘ§”κ÷ΛΖ®“Μ
Ά§άμΩ…ΒΟ![]()
![]() Θ°
Θ°
![]()
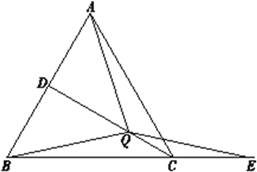
Θ®2Θ©»γΆΦ12Θ§Β±30ΓψΘΦΠΝΘΦ60Γψ ±Θ§![]() Θ°
Θ°


 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΫΪΤΫ––ΥΡ±Ώ–ΈABCD―ΊΕ‘Ϋ«œΏBDΫχ––’έΒΰΘ§’έΒΰΚσΒψC¬δ‘ΎΒψF¥ΠΘ§DFΫΜAB”ΎΒψEΘ°
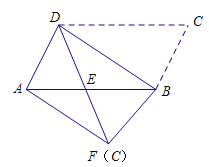
Θ®1Θ©«σ÷ΛΘΚ![]() ΘΜ
ΘΜ
Θ®2Θ©≈–ΕœAF”κBD «ΖώΤΫ––Θ§≤ΔΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈε“ΜΦΌΤΎΡ≥―ß–ΘΦΤΜ°Ήι÷·385Οϊ Π…ζΉβ≥¬ϔΈΘ§œ÷÷ΣΒά≥ωΉβΙΪΥΨ”–42ΉυΚΆ60ΉυΩΆ≥ΒΘ§ΟΩΝΨ42Ήυ±»ΟΩΝΨ60ΉυΩΆ≥ΒΉβΫπ±ψ“Υ140‘ΣΘ§Ήβ3ΝΨ42ΉυΚΆ2ΟΩΝΨ60ΉυΩΆ≥ΒΉβΫπΙ≤ΦΤ1880‘Σ
(1) «σΝΫ÷÷≥ΒΉβΫπΟΩΝΨΗςΕύ…Ό‘ΣΘΩ
(2) »τ―ß–ΘΆ§ ±Ήβ”Ο’βΝΫ÷÷ΩΆ≥Β8ΝΨΘ®Ω…“‘Ήχ≤Μ¬ζΘ©Θ§ΉήΉβΫπ≤Μ≥§Ιΐ3200‘ΣΘ§”–ΦΗ÷÷Ήβ≥ΒΖΫΑΗΘΩ«κ―Γ‘ώΉνΫΎ ΓΒΡΉβ≥ΒΖΫΑΗ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§Κ· ΐ![]() Θ®
Θ®![]() Θ©ΒΡΆΦœσΨ≠ΙΐΒψ
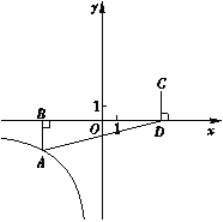
Θ©ΒΡΆΦœσΨ≠ΙΐΒψ![]() Θ§ABΓΆx÷α”ΎΒψBΘ§ΒψC”κΒψAΙΊ”Ύ‘≠ΒψOΕ‘≥ΤΘ§ CDΓΆx÷α”ΎΒψDΘ§ΓςABDΒΡΟφΜΐΈΣ8.
Θ§ABΓΆx÷α”ΎΒψBΘ§ΒψC”κΒψAΙΊ”Ύ‘≠ΒψOΕ‘≥ΤΘ§ CDΓΆx÷α”ΎΒψDΘ§ΓςABDΒΡΟφΜΐΈΣ8.
Θ®1Θ©«σmΘ§nΒΡ÷ΒΘΜ
Θ®2Θ©»τ÷±œΏ![]() Θ®kΓΌ0Θ©Ψ≠ΙΐΒψCΘ§«“”κx÷αΘ§y÷αΒΡΫΜΒψΖ÷±πΈΣΒψEΘ§FΘ§Β±
Θ®kΓΌ0Θ©Ψ≠ΙΐΒψCΘ§«“”κx÷αΘ§y÷αΒΡΫΜΒψΖ÷±πΈΣΒψEΘ§FΘ§Β±![]() ±Θ§«σΒψFΒΡΉχ±ξΘ°
±Θ§«σΒψFΒΡΉχ±ξΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΝβ–Έ![]() ÷–Θ§
÷–Θ§![]() .«κΗυΨίœ¬Ν–ΧθΦΰΘ§Ϋω”ΟΈόΩΧΕ»ΒΡ÷±≥ΏΙΐΕΞΒψ
.«κΗυΨίœ¬Ν–ΧθΦΰΘ§Ϋω”ΟΈόΩΧΕ»ΒΡ÷±≥ΏΙΐΕΞΒψ![]() ΉςΝβ–Έ
ΉςΝβ–Έ![]() ΒΡ±Ώ
ΒΡ±Ώ![]() …œΒΡΗΏΓΘ
…œΒΡΗΏΓΘ

Θ®1Θ©‘ΎΆΦ1÷–Θ§Βψ![]() ΈΣ
ΈΣ![]() ÷–ΒψΘΜ
÷–ΒψΘΜ
Θ®2Θ©‘ΎΆΦ2÷–Θ§Βψ![]() ΈΣ
ΈΣ![]() ÷–Βψ.
÷–Βψ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§Ρ≥ΒΊΖΫ’ΰΗ°ΨωΕ®‘ΎœύΨύ50kmΒΡAΓΔBΝΫ’Ψ÷°ΦδΒΡΙΪ¬Ζ≈‘EΒψΘ§–όΫ®“ΜΗωΆΝΧΊ≤ζΦ”ΙΛΜυΒΊΘ§«“ ΙCΓΔDΝΫ¥εΒΫEΒψΒΡΨύάκœύΒ»Θ§“―÷ΣDAΓΆAB”ΎAΘ§CBΓΆAB”ΎBΘ§DA=30kmΘ§CB=20kmΘ§Ρ«Ο¥ΜυΒΊE”ΠΫ®‘ΎάκA’ΨΕύ…Ό«ßΟΉΒΡΒΊΖΫΘΩ

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΨΊ–Έ![]() ÷–ΘΜΒψ
÷–ΘΜΒψ![]() ΈΣΉχ±ξ‘≠ΒψΘ§Βψ
ΈΣΉχ±ξ‘≠ΒψΘ§Βψ![]() Θ§Βψ
Θ§Βψ![]() ΓΔ
ΓΔ![]() ‘ΎΉχ±ξ÷α…œΘ§Βψ
‘ΎΉχ±ξ÷α…œΘ§Βψ![]() ‘Ύ
‘Ύ![]() ±Ώ…œΘ§÷±œΏ
±Ώ…œΘ§÷±œΏ![]() ΫΜ
ΫΜ![]() ÷α”ΎΒψ
÷α”ΎΒψ![]() .Ε‘”ΎΉχ±ξΤΫΟφΡΎΒΡ÷±œΏΘ§œ»ΫΪΗΟ÷±œΏœρ”“ΤΫ“Τ
.Ε‘”ΎΉχ±ξΤΫΟφΡΎΒΡ÷±œΏΘ§œ»ΫΪΗΟ÷±œΏœρ”“ΤΫ“Τ![]() ΗωΒΞΈΜ≥ΛΕ»Θ§‘Όœρœ¬ΤΫ“Τ
ΗωΒΞΈΜ≥ΛΕ»Θ§‘Όœρœ¬ΤΫ“Τ![]() ΗωΒΞΈΜ≥ΛΕ»Θ§’β÷÷÷±œΏ‘ΥΕ·≥ΤΈΣ÷±œΏΒΡ–±ΤΫ“Τ.œ÷ΫΪ÷±œΏ
ΗωΒΞΈΜ≥ΛΕ»Θ§’β÷÷÷±œΏ‘ΥΕ·≥ΤΈΣ÷±œΏΒΡ–±ΤΫ“Τ.œ÷ΫΪ÷±œΏ![]() Ψ≠Ιΐ
Ψ≠Ιΐ![]() ¥Έ–±ΤΫ“ΤΘ§ΒΟΒΫ÷±œΏ
¥Έ–±ΤΫ“ΤΘ§ΒΟΒΫ÷±œΏ![]() .
.


Θ®±Η”ΟΆΦΘ©
Θ®1Θ©«σ÷±œΏ![]() ”κΝΫΉχ±ξ÷αΈß≥…ΒΡΟφΜΐΘΜ
”κΝΫΉχ±ξ÷αΈß≥…ΒΡΟφΜΐΘΜ
Θ®2Θ©«σ÷±œΏ![]() ”κ
”κ![]() ΒΡΫΜΒψΉχ±ξΘΜ
ΒΡΫΜΒψΉχ±ξΘΜ
Θ®3Θ©‘ΎΒΎ“ΜœσœόΡΎΘ§‘Ύ÷±œΏ![]() …œ «Ζώ¥φ‘Ύ“ΜΒψ
…œ «Ζώ¥φ‘Ύ“ΜΒψ![]() Θ§ ΙΒΟ
Θ§ ΙΒΟ![]() «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘΩ»τ¥φ‘ΎΘ§«κ÷±Ϋ”–¥≥ωΒψ
«Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘΩ»τ¥φ‘ΎΘ§«κ÷±Ϋ”–¥≥ωΒψ![]() ΒΡΉχ±ξΘ§»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
ΒΡΉχ±ξΘ§»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩœ÷ΫΪ»ΐ’≈–ΈΉ¥ΓΔ¥σ–ΓΆξ»ΪœύΆ§ΒΡΤΫ––ΥΡ±Ώ–ΈΆΗΟς÷ΫΤ§Ζ÷±πΖ≈‘ΎΖΫΗώ÷Ϋ÷–Θ§ΖΫΗώ÷Ϋ÷–ΒΡΟΩΗω–Γ’ΐΖΫ–ΈΒΡ±Ώ≥ΛΨυΈΣ1Θ§≤Δ«“ΤΫ––ΥΡ±Ώ–Έ ÷ΫΤ§ΒΡΟΩΗωΕΞΒψ”κ–Γ’ΐΖΫ–ΈΒΡΕΞΒψ÷ΊΚœ(»γΆΦΔΌΓΔΆΦΔΎΓΔΆΦΔέ)Θ°


ΆΦΔΎΨΊ–Έ(’ΐΖΫ–Έ)
 ,
,
Ζ÷±π‘ΎΆΦΔΌΓΔΆΦΔΎΓΔΆΦΔέ÷–Θ§Ψ≠ΙΐΤΫ––ΥΡ±Ώ–Έ÷ΫΤ§ΒΡ»Έ“β“ΜΗωΕΞΒψΜ≠“ΜΧθ≤ΟΦτœΏΘ§―Ί¥Υ≤ΟΦτœΏΫΪΤΫ––ΥΡ±Ώ–Έ÷ΫΤ§≤Ο≥…ΝΫ≤ΩΖ÷Θ§≤ΔΑ―’βΝΫ≤ΩΖ÷÷Ί–¬Τ¥≥…ΖϊΚœœ¬Ν–“Σ«σΒΡΦΗΚΈΆΦ–ΈΘ°
“Σ«σΘΚ
(1)‘ΎΉσ±ΏΒΡΤΫ––ΥΡ±Ώ–Έ÷ΫΤ§÷–Μ≠“ΜΧθ≤ΟΦτœΏΘ§»ΜΚσ‘Ύ”“±ΏœύΕ‘”ΠΒΡΖΫΗώ÷Ϋ÷–Θ§Α¥ ΒΦ ¥σ–ΓΜ≠≥ωΥυΤ¥≥…ΒΡΖϊΚœ“Σ«σΒΡΦΗΚΈΆΦ–ΈΘ°
(2)≤Ο≥…ΒΡΝΫ≤ΩΖ÷‘ΎΤ¥≥…ΦΗΚΈΆΦ–Έ ±“ΣΜΞ≤Μ÷ΊΒΰ«“≤ΜΝτΩ’œΕΘ°
(3)ΥυΜ≠≥ωΒΡΦΗΚΈΆΦ–ΈΒΡΗςΕΞΒψ±Ί–κ”κ–Γ’ΐΖΫ–ΈΒΡΕΞΒψ÷ΊΚœΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥–Θ―ß…ζ ΐ―ß–Υ»Λ–ΓΉιΈΣΝΥΫβ±Ψ–ΘΆ§―ßΕ‘…œΩΈΆβ≤ΙœΑΑύΒΡΧ§Ε»Θ§‘Ύ―ß–Θ≥ι»ΓΝΥ≤ΩΖ÷Ά§―ßΫχ––ΝΥΈ ΨμΒς≤ιΘ§Βς≤ιΖ÷±πΈΣΓΑA©¹Ζ«≥Θ‘όΆ§Γ±ΓΔΓΑB©¹‘όΆ§Γ±ΓΔΓΑC©¹ΈόΥυΈΫΓ±ΓΔΓΑD©¹≤Μ‘όΆ§Γ±Β»ΥΡ÷÷Χ§Ε»Θ§œ÷ΫΪΒς≤ιΆ≥ΦΤΫαΙϊ÷Τ≥…ΝΥ»γΆΦΝΫΖυΆ≥ΦΤΆΦΘ§«κΫαΚœΝΫΖυΆ≥ΦΤΆΦΘ§ΜΊ¥πœ¬Ν–Έ ΧβΘΚ
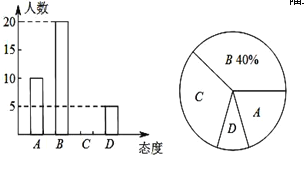
Θ®1Θ©≥ι»ΓΝΥΕύ…ΌΟϊΆ§―ßΫχ––ΝΥΈ ΨμΒς≤ιΘΩ
Θ®2Θ©«κ≤Ι»ΪΧθ–ΈΆ≥ΦΤΆΦΘ°
Θ®3Θ©≥÷ΓΑ≤Μ‘όΆ§Γ±Χ§Ε»ΒΡ―ß…ζ»Υ ΐΒΡΑΌΖ÷±»Υυ’Φ…»–ΈΒΡ‘≤–ΡΫ«ΈΣΓΓ ΓΓΕ»Θ°
Θ®4Θ©»τΗΟ–Θ”–3000Οϊ―ß…ζΘ§«κΡψΙάΦΤΗΟ–Θ―ß…ζΕ‘≥÷ΓΑ‘όΆ§Γ±ΚΆΓΑΖ«≥Θ‘όΆ§Γ±ΝΫ÷÷Χ§Ε»ΒΡ»Υ ΐ÷°ΚΆΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com