练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在菱形中，.请根据下列条件，仅用无刻度的直尺过顶点作菱形的边上的高。

    （1）在图1中，点为中点；

    （2）在图2中，点为中点.

    【答案】（1）见解析；（2）见解析.

    【解析】

    （1）在菱形中，，可知△ACD是等边三角形，过顶点作菱形的边上的高，即找到AD的边中点即可.根据菱形是中心对称图形，连接AC、BD得到对称中心O，再作直线交于，连接，即可.

    （2）在菱形中，，可知△ACD是等边三角形，过顶点作菱形的边上的高，即找到AD的边中点即可.根据菱形是轴对称图形，连接，交于点，作直线交于，线段即为所求．

    解：（1）如图1中，连接，交于点，作直线交于，连接，线段即为所求．

    （2）如图2中，连接，交于点，作直线交于，线段即为所求．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

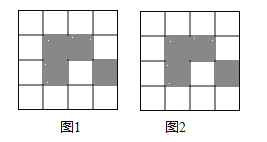
    【题目】如图，下列4×4网格图都是由16个相同小正方形组成，每个网格图中有4个小正方形已涂上阴影，请在空白小正方形中，按下列要求涂上阴影．

    （1）在图1中选取2个空白小正方形涂上阴影，使6个阴影小正方形组成一个中心对称图形；

    （2）在图2中选取2个空白小正方形涂上阴影，使6个阴影小正方形组成一个轴对称图形，但不是中心对称图形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线y=a（x+3）（x﹣1）（a≠0），与x轴从左至右依次相交于A、B两点，与y轴相交于点C，经过点A的直线y=﹣x+b与抛物线的另一个交点为D．

    （1）若点D的横坐标为2，求抛物线的函数解析式；

    （2）若在第三象限内的抛物线上有点P，使得以A、B、P为顶点的三角形与△ABC相似，求点P的坐标；

    （3）在（1）的条件下，设点E是线段AD上的一点（不含端点），连接BE．一动点Q从点B出发，沿线段BE以每秒1个单位的速度运动到点E，再沿线段ED以每秒个单位的速度运动到点D后停止，问当点E的坐标是多少时，点Q在整个运动过程中所用时间最少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

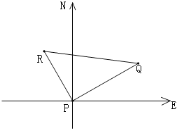
    【题目】如图，某港口P位于东西方向的海岸线上，“远航”号、“海天”号轮船同时离开港口，各自沿一固定方向航行，“远航”号每小时航行16海里，“海天”号每小时航行12海里．它们离开港口一个半小时后，分别位于点Q、R处，且相距30海里，如果知道“远航”号沿北偏东方向航行，请求出“海天”号的航行方向？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某地2016年为做好“精准扶贫”，投入资金1280万元用于异地安置，并规划投入资金逐年增加，2018年在2016年的基础上增加投入资金1600万元．

    （1）从2016年到2018年，该地投入异地安置资金的年平均增长率为多少？

    （2）在2018年异地安置的具体实施中，该地计划投入资金不低于500万元用于优先搬迁租房奖励，规定前800户（含第800户）每户每天奖励10元，800户以后每户每天奖励5元，按租房400天计算，求2018年该地至少有多少户享受到优先搬迁租房奖励．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在等边三角形ABC中，CD为中线，点Q在线段CD上运动，将线段QA绕点Q顺时针旋转，使得点A的对应点E落在射线BC上，连接BQ，设∠DAQ=α

    （0°＜α＜60°且α≠30°）.

    （1）当0°＜α＜30°时，

    ①在图1中依题意画出图形，并求∠BQE（用含α的式子表示）；

    ②探究线段CE，AC，CQ之间的数量关系，并加以证明；

    （2）当30°＜α＜60°时，直接写出线段CE，AC，CQ之间的数量关系.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，是直线上的一点，射线，分别平分和．

    （1）与相等的角有_____________；

    （2）与互余的角有______________；

    （3）已知，求的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知，点在边上，.过点作于点，以为一边在内作等边，点是围成的区域（包括各边）内的一点，过点作交于点，作交于点.设，，则最大值是_______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有一些相同的房间需要粉刷墙面．一天3名一级技工去粉刷8个房间,结果其中有50m2墙面未来得及粉刷;同样时间内5名二级技工粉刷了10个房间之外,还多粉刷了另外的40m2墙面．每名一级技工比二级技工一天多粉刷12m2墙面，求一个一级技工和一个二级技工每天粉刷的墙面各是多少．

    查看答案和解析>>

    同步练习册答案