
����Ŀ��ij��2016��Ϊ����������ƶ����Ͷ���ʽ�1280��Ԫ������ذ��ã����滮Ͷ���ʽ��������ӣ�2018����2016��Ļ���������Ͷ���ʽ�1600��Ԫ��
��1����2016�굽2018�꣬�õ�Ͷ����ذ����ʽ����ƽ��������Ϊ���٣�
��2����2018����ذ��õľ���ʵʩ�У��õؼƻ�Ͷ���ʽ���500��Ԫ�������Ȱ�Ǩ�ⷿ�������涨ǰ800��������800����ÿ��ÿ�콱��10Ԫ��800���Ժ�ÿ��ÿ�콱��5Ԫ�����ⷿ400����㣬��2018��õ������ж��ٻ����ܵ����Ȱ�Ǩ�ⷿ������
���𰸡���1����2016�굽2018�꣬�õ�Ͷ����ذ����ʽ����ƽ��������Ϊ50%����2��2018��õ�������1700�����ܵ����Ȱ�Ǩ�ⷿ����.
��������
��1������ƽ��������Ϊx�����ݣ�2016��Ͷ���ʽ�����1+�����ʣ�2=2018��Ͷ���ʽ��г��������ɵã�
��2����2018��õ���a�����ܵ����Ȱ�Ǩ�ⷿ���������ݣ�ǰ800����õĽ�������+800���Ժ��õĽ����ܺ���500���в���ʽ���ɵã�
��1����õ�Ͷ����ذ����ʽ����ƽ��������Ϊx��
��������ã�![]()
���![]() ��
��![]() ���������⣬��ȥ����
���������⣬��ȥ����
�𣺴�2016�굽2018�꣬�õ�Ͷ����ذ����ʽ����ƽ��������Ϊ50%��
��2����2018��õ���a�����ܵ����Ȱ�Ǩ�ⷿ������
��������ã�![]() ��
��
��ã�![]() ��
��
��2018��õ�������1700�����ܵ����Ȱ�Ǩ�ⷿ������


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ��������
������ͼ��
���壺��ij��ͼ�οɷָ�Ϊ���ɸ����������Ƶ�ͼ�Σ�������ͼ����������ͼ�Σ����磺������ABCD�У���E��F��G��H�ֱ���AB��BC��CD��DA�ߵ��е㣬����EG��HF���ڵ�O����֪�ָ�ɵ��ĸ��ı���AEOH��EBFO��OFCG��HOGD��Ϊ�����Σ�����ԭ���������ƣ�����������������ͼ�Σ�
����
��1��ͼ1��������ABCD�ָ�ɵ��ĸ�С�������У�ÿ����������ԭ�����ε����Ʊ�Ϊ�� ����
��2����ͼ2����֪��ABC�У���ACB=90�㣬AC=4��BC=3��С��������ABCҲ�ǡ�������ͼ�Ρ�������˼·�ǣ�����C��CD��AB�ڵ�D����CD����ABC�ָ��2�������Լ����Ƶ�Сֱ�������Σ���֪��ACD�ס�ABC������ACD����ABC�����Ʊ�Ϊ�� ����
��3������һ������ABCD��������ͼ�Σ����г�AD=a����AB=b��a��b����
�������A��B��������ѡһ��������ѡ���� ���⣮
A������ͼ3��1����������ABCD����ָ������ȫ�Ⱦ��Σ�����ԭ���ζ����ƣ���a=�� �����ú�b��ʽ�ӱ�ʾ����
����ͼ3��2��������ABCD����ָ��n��ȫ�Ⱦ��Σ�����ԭ���ζ����ƣ���a=�� �����ú�n��b��ʽ�ӱ�ʾ����
B������ͼ4��1����������ABCD������ָ��2��ȫ�Ⱦ��Σ��ٽ�ʣ��IJ��ֺ���ָ��3��ȫ�Ⱦ��Σ��ҷָ�õ��ľ�����ԭ���ζ����ƣ���a=�� �����ú�b��ʽ�ӱ�ʾ����
����ͼ4��2����������ABCD������ָ��m��ȫ�Ⱦ��Σ��ٽ�ʣ��IJ��ֺ���ָ��n��ȫ�Ⱦ��Σ��ҷָ�õ��ľ�����ԭ���ζ����ƣ���a=�� �����ú�m��n��b��ʽ�ӱ�ʾ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ij��2017����ҵ��ˮ��x���֣������Ӧ����ˮ��y��Ԫ��֮��ĺ�����ϵ��ͼ��ʾ��
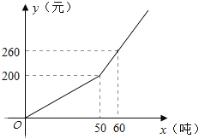
��1����y����x�ĺ�����ϵʽ��
��2����ij��ҵ2017��10�·ݵ�ˮ��Ϊ620Ԫ�������ҵ2017��10�·ݵ���ˮ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У���DBC=90������ABD=30������ADB=75����AC��BD���ڵ�E����CE=2AE=4![]() ����DC�ij�Ϊ________��
����DC�ij�Ϊ________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���˼ƻ��ӹ�һ����Ʒ�����ÿСʱ�ӹ���Ʒ10�����Ϳ�����Ԥ��ʱ������������ÿСʱ��ӹ�2�����Ϳ�����ǰ1Сʱ�������
��1���ò�Ʒ��Ԥ���ӹ�ʱ��Ϊ��Сʱ��
��2�����ò�Ʒ����ʱ�ı��Ϊ100Ԫ/��������۵İ�������ʱ��ÿ���Կ���ӯ��25Ԫ��������Ʒ�ܳɱ�Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ƽ��ֱ������ϵ�У�����OABC�ı�OA��OC�ֱ���x��������ᡢy����������ϣ���OA��OC��![]() ���ij��Ƿ���
���ij��Ƿ���![]() ����������
����������
��1����ͼ�����A�����ꣻ
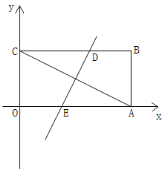
��2����ͼ��������OABC��ij��ֱ���۵���ʹ��A���C�غϣ��ۺ۽�CB�ڵ�D����OA�ڵ�E����ֱ��DE�Ľ���ʽ��

��3���ڣ�2���������£���P��ֱ��DE�ϣ���ֱ��AC���Ƿ���ڵ�Q��ʹ�Ե�A��B��P��QΪ������ı�����ƽ���ı��Σ������ڣ��������Q���ꣻ�������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
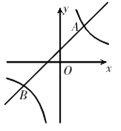
����Ŀ����ͼ��һ�κ��� y=k x+b �뷴�������� ![]() ͼ���ڵ� A (2��m) �͵� B��n��-2��.
ͼ���ڵ� A (2��m) �͵� B��n��-2��.
��1�� ���һ�κ�������ʽ��m��n��ֵ��
��2�� ���ͼ����ʽ![]() �Ľ⼯.
�Ľ⼯.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס����������̶Ӽƻ���һ����15ǧ����幫·����֪���̶�ÿ����ҹ��̶�ÿ�����·0.5ǧ�ף��ҹ��̶ӵ��������·�������������Ǽ��̶ӵ��������·��������������1.5����
��1����ס����������̶�ÿ�����·����ǧ�ף�
��2�������̶�ÿ�����·����Ϊ0.5��Ԫ���ҹ��̶�ÿ�����·����Ϊ0.4��Ԫ��Ҫʹ�������̶���·�ܷ��ò�����5.2��Ԫ�����̶�������·�����죿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһƽ���ڣ�����ֱ���ཻʱ�����1�����㣬����ֱ���ཻʱ�����3�����㣬����ֱ���ཻʱ�����6�����㣬������ôʮ��ֱ���ཻʱ�����____�����㣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com