
【题目】已知,在平面直角坐标系中,矩形OABC的边OA、OC分别在x轴的正半轴、y轴的正半轴上,且OA、OC(![]() )的长是方程
)的长是方程![]() 的两个根.
的两个根.
(1)如图,求点A的坐标;
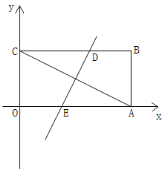
(2)如图,将矩形OABC沿某条直线折叠,使点A与点C重合,折痕交CB于点D,交OA于点E.求直线DE的解析式;

(3)在(2)的条件下,点P在直线DE上,在直线AC上是否存在点Q,使以点A、B、P、Q为顶点的四边形是平行四边形.若存在,请求出点Q坐标;若不存在,请说明理由.
【答案】(1)(8,0);(2)![]() ;(3)存在点
;(3)存在点![]() 或
或![]() 或
或![]() ,使以点A、B、P、Q为顶点的四边形是平行四边形.
,使以点A、B、P、Q为顶点的四边形是平行四边形.
【解析】
(1)通过解一元二次方程可求出OA的长,结合点A在x轴正半轴可得出点A的坐标;
(2)连接CE,设OE=m,则AE=CE=8-m,在Rt△OCE中,利用勾股定理可求出m的值,进而可得出点E的坐标,同理可得出点D的坐标,根据点D,E的坐标,利用待定系数法可求出直线DE的解析式;
(3)根据点A,C的坐标,利用待定系数法可求出直线AC的解析式,设点P的坐标为(a,2a-6),点Q的坐标为(c,-![]() c+4),分AB为边和AB为对角线两种情况考虑:①当AB为边时,利用平行四边形的性质可得出关于a,c的二元一次方程组,解之可得出c值,再将其代入点Q的坐标中即可得出结论;②当AB为对角线时,利用平行四边形的对角线互相平分,可得出关于a,c的二元一次方程组,解之可得出c值,再将其代入点Q的坐标中即可得出结论.综上,此题得解.
c+4),分AB为边和AB为对角线两种情况考虑:①当AB为边时,利用平行四边形的性质可得出关于a,c的二元一次方程组,解之可得出c值,再将其代入点Q的坐标中即可得出结论;②当AB为对角线时,利用平行四边形的对角线互相平分,可得出关于a,c的二元一次方程组,解之可得出c值,再将其代入点Q的坐标中即可得出结论.综上,此题得解.
(1)解方程x2-12x+32=0,得:x1=4,x2=8.
∵OA、OC的长是方程x2-12x+32=0的两个根,且OA>OC,点A在x轴正半轴上,
∴点A的坐标为(8,0).
(2)连接CE,如图4所示.
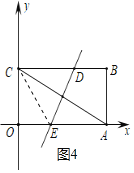
由(1)可得:点C的坐标为(0,4),点B的坐标为(8,4).
设OE=m,则AE=CE=8-m.
在Rt△OCE中,∠COE=90°,OC=4,OE=m,
∴CE2=OC2+OE2,即(8-m)2=42+m2,
解得:m=3,
∴OE=3,
∴点E的坐标为(3,0).
同理,可求出BD=3,
∴点D的坐标为(5,4).
设直线DE解析式为:![]()
![]()
∴![]()
∴直线DE解析式为:![]()
(3)∵点A的坐标为(8,0),点C的坐标为(0,4),点B的坐标为(8,4),
∴直线AC的解析式为y=-![]() x+4,AB=4.
x+4,AB=4.
设点P的坐标为(a,2a-6),点Q的坐标为(c,-![]() c+4).
c+4).
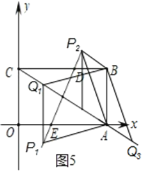
分两种情况考虑,如图5所示:
①当AB为边时,  ,
,
解得:c1=![]() ,c2=
,c2=![]() ,
,
∴点Q1的坐标为(![]() ,
,![]() ),点Q2的坐标为(
),点Q2的坐标为(![]() ,
,![]() );
);
②当AB为对角线时,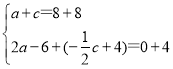 ,
,
解得: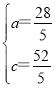 ,
,
∴点Q3的坐标为(![]() ,-
,- ![]() ).
).
综上,存在点![]() 或
或![]() 或
或![]() ,使以点A、B、P、Q为顶点的四边形是平行四边形
,使以点A、B、P、Q为顶点的四边形是平行四边形


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:初中数学 来源: 题型:
【题目】为了解黔东南州某县2013届中考学生的体育考试得分情况,从该县参加体育考试的4000名学生中随机抽取了100名学生的体育考试成绩作样本分析,得出如下不完整的频数统计表和频数分布直方图.
成绩分组 | 组中值 | 频数 |
25≤x<30 | 27.5 | 4 |
30≤x<35 | 32.5 | m |
35≤x<40 | 37.5 | 24 |
40≤x<45 | a | 36 |
45≤x<50 | 47.5 | n |
50≤x<55 | 52.5 | 4 |
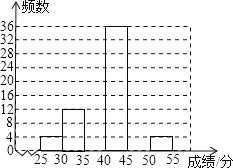
(1)求a、m、n的值,并补全频数分布直方图;
(2)若体育得分在40分以上(包括40分)为优秀,请问该县中考体育成绩优秀学生人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
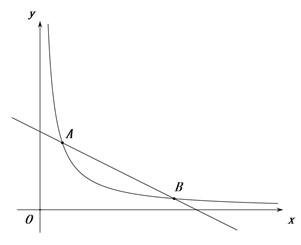
【题目】如图,一次函数y=-![]() x+b与反比例函数y=
x+b与反比例函数y=![]() (x>0)的图象交于点A(2,6)和B(m,1)
(x>0)的图象交于点A(2,6)和B(m,1)
(1)填空:一次函数的解析式为 ,反比例函数的解析式为 ;
(2)点E为y轴上一个动点,若S△AEB=5,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每个图案均由边长相等的黑、白两色正方形按规律拼接而成,照此规律,第n个图案中白色正方形比黑色正方形多________个.(用含n的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地2016年为做好“精准扶贫”,投入资金1280万元用于异地安置,并规划投入资金逐年增加,2018年在2016年的基础上增加投入资金1600万元.
(1)从2016年到2018年,该地投入异地安置资金的年平均增长率为多少?
(2)在2018年异地安置的具体实施中,该地计划投入资金不低于500万元用于优先搬迁租房奖励,规定前800户(含第800户)每户每天奖励10元,800户以后每户每天奖励5元,按租房400天计算,求2018年该地至少有多少户享受到优先搬迁租房奖励.
查看答案和解析>>
科目:初中数学 来源: 题型:
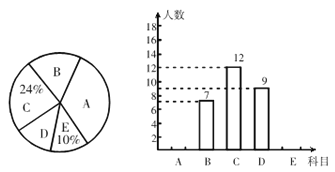
【题目】海珠区某学校为进一步加强和改进学校体育工作,切实提高学生体质健康水平,决定推进“一人一球”活动计划. 学生可根据自己的喜好选修一门球类项目(A :足球,B:篮球,C:排球,D:羽毛球,E:乒乓球),陈老师对某班全班同学的
选课情况进行统计后,制成了两幅不完整的统计图 (如图).
(1) 求出该班的总人数,并将条形统计图补充完整;
(2) 若该校共有学生 2500 名,请估计约有多少人选修足球?
(3) 该班班委 4 人中,1 人选修足球,1 人选修篮球,2 人选修羽毛球,陈老师要从这
4 人中任选 2 人了解他们对体育选修课的看法,请你用列表或画树状图的方法,求 选出的 2 人中至少有 1 人选修羽毛球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某中学2018年田径运动会上,参加跳高的运动员的成绩如表三所示.
成绩/m | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
人数 | 2 | 3 | 2 | 3 | 4 | 1 |
(1)写出这些运动员跳高成绩的众数;
(2)该按2017年田径运动会上跳高的平均成绩为1.63m,则该校2018年田径运动会上跳高的平均成绩与2017年相比,是否有提高?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com