
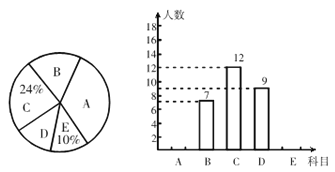
【题目】海珠区某学校为进一步加强和改进学校体育工作,切实提高学生体质健康水平,决定推进“一人一球”活动计划. 学生可根据自己的喜好选修一门球类项目(A :足球,B:篮球,C:排球,D:羽毛球,E:乒乓球),陈老师对某班全班同学的
选课情况进行统计后,制成了两幅不完整的统计图 (如图).
(1) 求出该班的总人数,并将条形统计图补充完整;
(2) 若该校共有学生 2500 名,请估计约有多少人选修足球?
(3) 该班班委 4 人中,1 人选修足球,1 人选修篮球,2 人选修羽毛球,陈老师要从这
4 人中任选 2 人了解他们对体育选修课的看法,请你用列表或画树状图的方法,求 选出的 2 人中至少有 1 人选修羽毛球的概率.
【答案】(1)见解析(2)850(3)![]()
【解析】分析:(1)、先利用C的人数和所占的百分比计算出全班人数,再利用E的百分比计算出E的人数,则用全班人数分别减去B、C、D、E的人数得到A的人数,补全统计图即可.
(2)根据样本估计总体,用![]() 表示全校学生对足球感兴趣的百分比,然后用2500乘以
表示全校学生对足球感兴趣的百分比,然后用2500乘以![]() 即可得到选修足球的人数;
即可得到选修足球的人数;
(4)先利用树状图展示所有12种等可能的结果数,找出选出的![]() 人至少1人选修羽毛球所占结果数,然后根据概率公式求解.
人至少1人选修羽毛球所占结果数,然后根据概率公式求解.
详解:(1)该班总人数是:该班人数为12÷24%=50(人),
答:该班总人数是50人.
则E类人数是:10%×50=5(人),
A类人数为:5071295=17(人),
补全条形统计图如图所示:
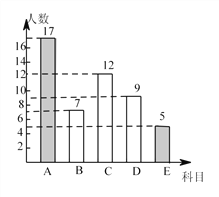
(2)选修足球的人数:![]() (人),
(人),
答:该校约有850人选修足球.
(3)用“ ![]() ”代表选修足球的1人,用“B ”代表选修篮球的1人,用“D1、D2”代表选修足球的2人,根据题意画出树状图如下:
”代表选修足球的1人,用“B ”代表选修篮球的1人,用“D1、D2”代表选修足球的2人,根据题意画出树状图如下:
由图可以看出,可能出现的结果有12种,并且它们出现的可能性相等.
其中至少1人选修羽毛球的结果有10种,
所以至少有 1 人选修羽毛球的概率![]()
答:选出的![]() 人至少1人选修羽毛球的概率为
人至少1人选修羽毛球的概率为![]()


 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:初中数学 来源: 题型:
【题目】阅读理解:
一般地,在数轴上点![]() ,
,![]() 表示的实数分别为
表示的实数分别为![]() ,
,![]() (
(![]() ),则
),则![]() ,
,![]() 两点的距离
两点的距离![]() .如图,在数轴上点
.如图,在数轴上点![]() ,
,![]() 表示的实数分别为-3,4,则记
表示的实数分别为-3,4,则记![]() ,
,![]() ,因为
,因为![]() ,显然
,显然![]() ,
,![]() 两点的距离
两点的距离![]() .
.
若点![]() 为线段
为线段![]() 的中点,则
的中点,则![]() ,所以
,所以![]() ,即
,即![]() .
.
解决问题:
(1)直接写出线段![]() 的中点
的中点![]() 表示的实数
表示的实数![]() ;
;
(2)在点![]() 右侧的数轴上有点
右侧的数轴上有点![]() ,且
,且![]() ,求点
,求点![]() 表示的实数
表示的实数![]() ;
;
(3)在(2)的条件下,点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 的中点,若
的中点,若![]() ,
,![]() 两点同时沿数轴向正方向运动,
两点同时沿数轴向正方向运动,![]() 点的速度是
点的速度是![]() 点速度的2倍,
点速度的2倍,![]() 的中点
的中点![]() 和
和![]() 的中点
的中点![]() 也随之运动,3秒后,
也随之运动,3秒后,![]() ,则点
,则点![]() 的速度为每秒 个单位长度.
的速度为每秒 个单位长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
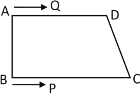
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=8cm,BC=10cm,AB=6cm,点Q从点A出发以1 cm/s的速度向点D运动,点P从点B出发以2 cm/s的速度向点C运动,P,Q两点同时出发,当点P到达点C时,两点同时停止运动.若设运动时间为t(s)
(1)直接写出:QD=______cm,PC=_______cm;(用含t的式子表示)
(2)当t为何值时,四边形PQDC为平行四边形?
(3)若点P与点C不重合,且DQ≠DP,当t为何值时,△DPQ是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
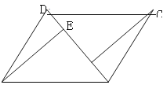
【题目】在![]() 中,BD是它的一条对角线,过A、C两点分别作
中,BD是它的一条对角线,过A、C两点分别作![]() ,
,![]() ,E、F为垂足.
,E、F为垂足.
(1)如图,求证:![]() ;
;
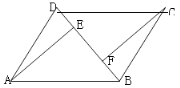
(2)如图,连接AC,设AC、BD交于点O,若![]() .在不添加任何辅助线的情况下,请直接写出图中的所有长度是OE长度2倍的线段.
.在不添加任何辅助线的情况下,请直接写出图中的所有长度是OE长度2倍的线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在平面直角坐标系中,矩形OABC的边OA、OC分别在x轴的正半轴、y轴的正半轴上,且OA、OC(![]() )的长是方程
)的长是方程![]() 的两个根.
的两个根.
(1)如图,求点A的坐标;
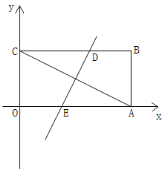
(2)如图,将矩形OABC沿某条直线折叠,使点A与点C重合,折痕交CB于点D,交OA于点E.求直线DE的解析式;

(3)在(2)的条件下,点P在直线DE上,在直线AC上是否存在点Q,使以点A、B、P、Q为顶点的四边形是平行四边形.若存在,请求出点Q坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文化用品商店用1 000元购进一批“晨光”套尺,很快销售一空;商店又用1 500元购进第二批该款套尺,购进时单价是第一批的![]() 倍,所购数量比第一批多100套.
倍,所购数量比第一批多100套.
(1)求第一批套尺购进时单价是多少?
(2)若商店以每套4元的价格将这两批套尺全部售出,可以盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)化简求值:(2+a)(2-a)+a(a-2b)+3a5b÷(-a2b)4,其中ab=-![]() .
.
(2)因式分解:a(n-1)2-2a(n-1)+a.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系xOy中的位置如图所示.
(1)作△ABC关于点C成中心对称的△A1B1C1;
(2)将△A1B1C1向右平移3个单位,作出平移后的△A2B2C2;
(3)在x轴上求作一点P,使PA1+PC2的值最小,并求最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形![]() 是平行四边形,点
是平行四边形,点![]() 在
在![]() 边上运动(点
边上运动(点![]() 不与点
不与点![]() ,
,![]() 重合)
重合)
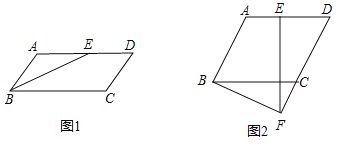
(1)如图1,当点![]() 运动到
运动到![]() 边的中点时,连接
边的中点时,连接![]() ,若
,若![]() 平分
平分![]() ,证明:
,证明:![]() ;
;
(2)如图2,过点![]() 作
作![]() 且交
且交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .若
.若![]() ,
,![]() ,
,![]() ,在线段
,在线段![]() 上是否存在一点
上是否存在一点![]() ,使得四边形
,使得四边形![]() 是菱形?若存在,请说明当发
是菱形?若存在,请说明当发![]() ,点
,点![]() 分别在线段
分别在线段![]() ,
,![]() 上什么位置时四边形
上什么位置时四边形![]() 是菱形,并证明;若不存在,请说明理由.
是菱形,并证明;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com