
【题目】为了解黔东南州某县2013届中考学生的体育考试得分情况,从该县参加体育考试的4000名学生中随机抽取了100名学生的体育考试成绩作样本分析,得出如下不完整的频数统计表和频数分布直方图.
成绩分组 | 组中值 | 频数 |
25≤x<30 | 27.5 | 4 |
30≤x<35 | 32.5 | m |
35≤x<40 | 37.5 | 24 |
40≤x<45 | a | 36 |
45≤x<50 | 47.5 | n |
50≤x<55 | 52.5 | 4 |
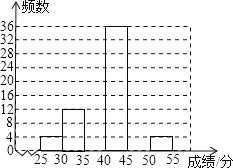
(1)求a、m、n的值,并补全频数分布直方图;
(2)若体育得分在40分以上(包括40分)为优秀,请问该县中考体育成绩优秀学生人数约为多少?
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】已知平面直角坐标系中两定点A(﹣1,0)、B(4,0),抛物线y=ax2+bx﹣2(a≠0)过点A,B,顶点为C,点P(m,n)(n<0)为抛物线上一点.
(1)求抛物线的解析式和顶点C的坐标;
(2)当∠APB为钝角时,求m的取值范围;
(3)若m>![]() ,当∠APB为直角时,将该抛物线向左或向右平移t(0<t<
,当∠APB为直角时,将该抛物线向左或向右平移t(0<t<![]() )个单位,点C、P平移后对应的点分别记为C′、P′,是否存在t,使得首位依次连接A、B、P′、C′所构成的多边形的周长最短?若存在,求t的值并说明抛物线平移的方向;若不存在,请说明理由.
)个单位,点C、P平移后对应的点分别记为C′、P′,是否存在t,使得首位依次连接A、B、P′、C′所构成的多边形的周长最短?若存在,求t的值并说明抛物线平移的方向;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2、C2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们用a表示不大于 a 的最大整数,用 a 表示大于 a 的最小整数.例如:2.5 2 ,3 3 , 2.5 3 ;<2.5> 3 ,<4> 5 ,< 1.5> 1 .解决下列问题:
(1) 4.5 ,< 3.5> .
(2)若x 2 ,则 < x> 的取值范围是 ;若< y > 1,则 y 的取值范围是 .
(3)已知 x, y 满足方程组![]() ;求 x, y 的取值范围.
;求 x, y 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成任务:
自相似图形
定义:若某个图形可分割为若干个都与它相似的图形,则称这个图形是自相似图形.例如:正方形ABCD中,点E、F、G、H分别是AB、BC、CD、DA边的中点,连接EG,HF交于点O,易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形,且与原正方形相似,故正方形是自相似图形.
任务:
(1)图1中正方形ABCD分割成的四个小正方形中,每个正方形与原正方形的相似比为 ;
(2)如图2,已知△ABC中,∠ACB=90°,AC=4,BC=3,小明发现△ABC也是“自相似图形”,他的思路是:过点C作CD⊥AB于点D,则CD将△ABC分割成2个与它自己相似的小直角三角形.已知△ACD∽△ABC,则△ACD与△ABC的相似比为 ;
(3)现有一个矩形ABCD是自相似图形,其中长AD=a,宽AB=b(a>b).
请从下列A、B两题中任选一条作答:我选择 题.
A:①如图3﹣1,若将矩形ABCD纵向分割成两个全等矩形,且与原矩形都相似,则a= (用含b的式子表示);
②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形,且与原矩形都相似,则a= (用含n,b的式子表示);
B:①如图4﹣1,若将矩形ABCD先纵向分割出2个全等矩形,再将剩余的部分横向分割成3个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含b的式子表示);
②如图4﹣2,若将矩形ABCD先纵向分割出m个全等矩形,再将剩余的部分横向分割成n个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含m,n,b的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
一般地,在数轴上点![]() ,
,![]() 表示的实数分别为
表示的实数分别为![]() ,
,![]() (
(![]() ),则
),则![]() ,
,![]() 两点的距离
两点的距离![]() .如图,在数轴上点
.如图,在数轴上点![]() ,
,![]() 表示的实数分别为-3,4,则记
表示的实数分别为-3,4,则记![]() ,
,![]() ,因为
,因为![]() ,显然
,显然![]() ,
,![]() 两点的距离
两点的距离![]() .
.
若点![]() 为线段
为线段![]() 的中点,则
的中点,则![]() ,所以
,所以![]() ,即
,即![]() .
.
解决问题:
(1)直接写出线段![]() 的中点
的中点![]() 表示的实数
表示的实数![]() ;
;
(2)在点![]() 右侧的数轴上有点
右侧的数轴上有点![]() ,且
,且![]() ,求点
,求点![]() 表示的实数
表示的实数![]() ;
;
(3)在(2)的条件下,点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 的中点,若
的中点,若![]() ,
,![]() 两点同时沿数轴向正方向运动,
两点同时沿数轴向正方向运动,![]() 点的速度是
点的速度是![]() 点速度的2倍,
点速度的2倍,![]() 的中点
的中点![]() 和
和![]() 的中点
的中点![]() 也随之运动,3秒后,
也随之运动,3秒后,![]() ,则点
,则点![]() 的速度为每秒 个单位长度.
的速度为每秒 个单位长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() 为数轴上的两个点,点
为数轴上的两个点,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() .
.

(1)现有一只电子蚂蚁![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度向左运动,同时另一只电子蚂蚁
个单位长度的速度向左运动,同时另一只电子蚂蚁![]() 恰好从点
恰好从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度向右运动,设两只电子蚂蚁在数轴上的点
个单位长度的速度向右运动,设两只电子蚂蚁在数轴上的点![]() 处相遇,求点
处相遇,求点![]() 表示的数;
表示的数;
(2)若电子蚂蚁![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度向左运动,同时另一电子蚂蚁
个单位长度的速度向左运动,同时另一电子蚂蚁![]() 恰好从点
恰好从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度向左运动,设两只电子蚂蚁在数轴上的点
个单位长度的速度向左运动,设两只电子蚂蚁在数轴上的点![]() 处相遇,求点
处相遇,求点![]() 表示的数.
表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在平面直角坐标系中,矩形OABC的边OA、OC分别在x轴的正半轴、y轴的正半轴上,且OA、OC(![]() )的长是方程
)的长是方程![]() 的两个根.
的两个根.
(1)如图,求点A的坐标;
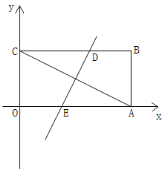
(2)如图,将矩形OABC沿某条直线折叠,使点A与点C重合,折痕交CB于点D,交OA于点E.求直线DE的解析式;

(3)在(2)的条件下,点P在直线DE上,在直线AC上是否存在点Q,使以点A、B、P、Q为顶点的四边形是平行四边形.若存在,请求出点Q坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com