
【题目】已知平面直角坐标系中两定点A(﹣1,0)、B(4,0),抛物线y=ax2+bx﹣2(a≠0)过点A,B,顶点为C,点P(m,n)(n<0)为抛物线上一点.
(1)求抛物线的解析式和顶点C的坐标;
(2)当∠APB为钝角时,求m的取值范围;
(3)若m>![]() ,当∠APB为直角时,将该抛物线向左或向右平移t(0<t<
,当∠APB为直角时,将该抛物线向左或向右平移t(0<t<![]() )个单位,点C、P平移后对应的点分别记为C′、P′,是否存在t,使得首位依次连接A、B、P′、C′所构成的多边形的周长最短?若存在,求t的值并说明抛物线平移的方向;若不存在,请说明理由.
)个单位,点C、P平移后对应的点分别记为C′、P′,是否存在t,使得首位依次连接A、B、P′、C′所构成的多边形的周长最短?若存在,求t的值并说明抛物线平移的方向;若不存在,请说明理由.
【答案】(1) 抛物线的解析式为:y=![]() x2﹣
x2﹣![]() x﹣2;C(
x﹣2;C( ![]() ,﹣
,﹣![]() ).(2) ﹣1<m<0或3<m<4;(3)
).(2) ﹣1<m<0或3<m<4;(3)![]()
【解析】分析:(1)待定系数法求解析式即可,求得解析式后转换成顶点式即可.
(2)因为AB为直径,所以当抛物线上的点P在⊙C的内部时,满足∠APB为钝角,所以-1<m<0,或3<m<4.
(3)左右平移时,使A′D+DB″最短即可,那么作出点C′关于x轴对称点的坐标为C″,得到直线P″C″的解析式,然后把A点的坐标代入即可.
详解:(1)∵抛物线y=ax2+bx﹣2(a≠0)过点A,B,
∴![]() ,
,
解得: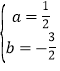 ,
,
∴抛物线的解析式为:y=![]() x2﹣
x2﹣![]() x﹣2;
x﹣2;
∵y=![]() x2﹣
x2﹣![]() x﹣2=
x﹣2=![]() (x﹣
(x﹣![]() )2﹣
)2﹣![]() ,
,
∴C(![]() ,﹣
,﹣![]() ).
).
(2)如图1,以AB为直径作圆M,则抛物线在圆内的部分,能使∠APB为钝角,
∴M(![]() ,0),⊙M的半径=
,0),⊙M的半径=![]() .
.
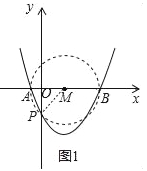
∵P′是抛物线与y轴的交点,
∴OP′=2,
∴MP′=![]() ,
,
∴P′在⊙M上,
∴P′的对称点(3,﹣2),
∴当﹣1<m<0或3<m<4时,∠APB为钝角.
(3)存在;
抛物线向左或向右平移,因为AB、P′C′是定值,所以A、B、P′、C′所构成的多边形的周长最短,只要AC′+BP′最小;
第一种情况:抛物线向右平移,AC′+BP′>AC+BP,
第二种情况:向左平移,如图2所示,由(2)可知P(3,﹣2),

又∵C(![]() ,﹣
,﹣![]() )
)
∴C'(![]() ﹣t,﹣
﹣t,﹣![]() ),P'(3﹣t,﹣2),
),P'(3﹣t,﹣2),
∵AB=5,
∴P″(﹣2﹣t,﹣2),
要使AC′+BP′最短,只要AC′+AP″最短即可,
点C′关于x轴的对称点C″(![]() ﹣t,
﹣t,![]() ),
),
设直线P″C″的解析式为:y=kx+b,
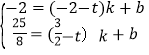 ,
,
解得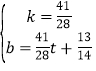
∴直线y=![]() ,
,
当P″、A、C″在一条直线上时,周长最小,
∴![]() =0
=0
∴t=![]() .
.
故将抛物线向左平移![]() 个单位连接A、B、P′、C′所构成的多边形的周长最短.
个单位连接A、B、P′、C′所构成的多边形的周长最短.


科目:初中数学 来源: 题型:
【题目】如图,等腰梯形ABCD中,AD∥BC,AD=7,AB=CD=15,BC=25,E为腰AB上一点且AE:BE=1:2,F为BC一动点,∠FEG=∠B,EG交射线BC于G,直线EG交射线CA于H.
(1)求sin∠ABC;
(2)求∠BAC的度数;
(3)设BF=x,CH=y,求y与x的函数关系式及其定义域.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场准备进一批两种不同型号的衣服,已知购进A种型号衣服9件,B种型号衣服10件,则共需1810元;若购进A种型号衣服12件,B种型号衣服8件,共需1880元;已知销售一件A型号衣服可获利18元,销售一件B型号衣服可获利30元,要使在这次销售中获利不少于699元,且A型号衣服不多于28件.
(1)求A、B型号衣服进价各是多少元?
(2)若已知购进A型号衣服是B型号衣服的2倍还多4件,则商店在这次进货中可有几种方案并简述购货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现在平均每天比原计划多生产 50 台机器,现在生产 600 台机器所需时间与原计划生产 450 台机器所需时间相同.
(1)现在平均每天生产多少台机器;
(2)生产 3000 台机器,现在比原计划提前几天完成.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学将组织七年级学生春游一天,由王老师和甲、乙两同学到客车租赁公司洽谈租车事宜.
(1)两同学向公司经理了解租车的价格,公司经理对他们说:“公司有45座和60座两种型号的客车可供租用,60座的客车每辆每天的租金比45座的贵100元.”王老师说:“我们学校八年级昨天在这个公司租了5辆45座和2辆60座的客车,一天的租金为1600元,你们能知道45座和60座的客车每辆每天的租金各是多少元吗”甲、乙两同学想了一下,都说知道了价格.
聪明的你知道45座和60座的客车每辆每天的租金各是多少元吗?
(2)公司经理问:“你们准备怎样租车”,甲同学说:“我的方案是只租用45座的客车,可是会有一辆客车空出30个座位”;乙同学说“我的方案只租用60座客车,正好坐满且比甲同学的方案少用两辆客车”,王老师在﹣旁听了他们的谈话说:“从经济角度考虑,还有别的方案吗”?如果是你,你该如何设计租车方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
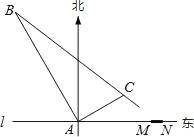
【题目】在东西方向的海岸线l上有一长为1km的码头MN(如图),在码头西端M的正西19.5km处有一观察站A.某时刻测得一艘匀速直线航行的轮船位于A的北偏西30°,且与A相距40km的B处;经过1小时20分钟,又测得该轮船位于A的北偏东60°,且与A相距![]() km的C处.
km的C处.
(1)求该轮船航行的速度(保留精确结果);
(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.
男、女生所选项目人数统计表
项目 | 男生(人数) | 女生(人数) |
机器人 | 7 | 9 |
3D打印 | m | 4 |
航模 | 2 | 2 |
其他 | 5 | n |
根据以上信息解决下列问题:
(1)m=_____,n=_____;
(2)扇形统计图中机器人项目所对应扇形的圆心角度数为_____°;
(3)从选航模项目的4名学生中随机选取2名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的2名学生中恰好有1名男生、1名女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
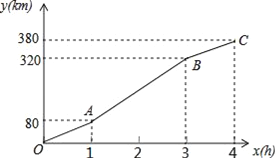
【题目】暑假期间,小刚一家乘车去离家380公里的某景区旅游,他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示.
(1)从小刚家到该景区乘车一共用了多少时间?
(2)求线段AB对应的函数解析式;
(3)小刚一家出发2.5小时时离目的地多远?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com