
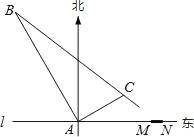
����Ŀ���ڶ�������ĺ�����l����һ��Ϊ1km����ͷMN����ͼ��������ͷ����M������19.5km����һ�۲�վA��ijʱ�̲��һ������ֱ�ߺ��е��ִ�λ��A�ı�ƫ��30��������A���40km��B��������1Сʱ20���ӣ��ֲ�ø��ִ�λ��A�ı�ƫ��60��������A���![]() km��C����
km��C����
��1������ִ����е��ٶȣ�������ȷ�������
��2��������ִ����ı亽��������У���ô�ִ��ܷ�����������ͷMN��������˵�����ɣ�
���𰸡���1��12![]() ��ǧ��/Сʱ������2�����ִ��ܹ�����������ͷMN������
��ǧ��/Сʱ������2�����ִ��ܹ�����������ͷMN������
�������������������1�����ݡ�1=30�㣬��2=60������֪��ABCΪֱ�������Σ����ݹ��ɶ������
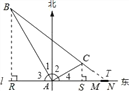
��2���ӳ�BC��l��T���Ƚ�AT��AM��AN�Ĵ�С���ɵó����ۣ�
�����������1���ߡ�1=30�㣬��2=60�㣬
���ABCΪֱ�������Σ�
��AB=40km��AC=![]() km��
km��
��BC=![]() ��km����
��km����
��1Сʱ20����=80���ӣ�1Сʱ=60���ӣ�
��![]() ��60=12
��60=12![]() ��ǧ��/Сʱ����
��ǧ��/Сʱ����
��2���ܣ�
���ɣ����߶�BR��AN��R�����߶�CS��AN��S���ӳ�BC��l��T��
�ߡ�2=60�㣬
���4=90�㩁60��=30�㣮
��AC=8![]() ��km����
��km����
��CS=8![]() sin30��=4
sin30��=4![]() ��km����
��km����
��AS=8![]() cos30��=8
cos30��=8![]() ��
��![]() =12��km����
=12��km����
�֡ߡ�1=30�㣬
���3=90�㩁30��=60�㣮
��AB=40km��
��BR=40sin60��=20![]() ��km����
��km����
��AR=40��cos60��=40��![]() =20��km����
=20��km����
�ã���STC�ס�RTB��
����![]() ��
��
![]() .
.
��ã�ST=8��km����
����AT=12+8=20��km����
����ΪAM=19.5km��MN��Ϊ1km����AN=20.5km��
��19.5��AT��20.5
���ִ��ܹ�����������ͷMN������


 ���ٴ�����ɽ����ϵ�д�
���ٴ�����ɽ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ����֯���꼶ѧ������һ����������ʦ�ͼס�����ͬѧ���ͳ�����˾Ǣ̸�������
��1����ͬѧ��˾�����˽���ļ۸�����˾����������˵������˾��45����60�������ͺŵĿͳ��ɹ�������60���Ŀͳ�ÿ��ÿ�������45���Ĺ�100Ԫ��������ʦ˵��������ѧУ���꼶�����������˾����5��45����2��60���Ŀͳ���һ������Ϊ1600Ԫ��������֪��45����60���Ŀͳ�ÿ��ÿ��������Ƕ���Ԫ�����ס�����ͬѧ����һ������˵֪���˼۸���
��������֪��45����60���Ŀͳ�ÿ��ÿ��������Ƕ���Ԫ��
��2����˾���������������������������ͬѧ˵�����ҵķ�����ֻ����45���Ŀͳ������ǻ���һ���ͳ��ճ�30����λ������ͬѧ˵���ҵķ���ֻ����60���ͳ������������ұȼ�ͬѧ�ķ������������ͳ���������ʦ�������������ǵ�̸��˵�����Ӿ��ýǶȿ��������б�ķ������������������������������������˵��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��CD��AB=CD����E��F��BC�ϣ���BF=CE��
��1����֤����ABE�ա�DCF��
��2����֤������A��F��D��EΪ������ı�����ƽ���ı��Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ƽ��ֱ������ϵ��������A����1��0����B��4��0����������y=ax2+bx��2��a��0������A��B������ΪC����P��m��n����n��0��Ϊ��������һ�㣮
��1���������ߵĽ���ʽ�Ͷ���C�����ꣻ
��2������APBΪ�۽�ʱ����m��ȡֵ��Χ��
��3����m��![]() ������APBΪֱ��ʱ���������������������ƽ��t��0��t��
������APBΪֱ��ʱ���������������������ƽ��t��0��t��![]() ������λ����C��Pƽ�ƺ��Ӧ�ĵ�ֱ��ΪC�䡢P�����Ƿ����t��ʹ����λ��������A��B��P�䡢C�������ɵĶ���ε��ܳ���̣������ڣ���t��ֵ��˵��������ƽ�Ƶķ����������ڣ���˵�����ɣ�
������λ����C��Pƽ�ƺ��Ӧ�ĵ�ֱ��ΪC�䡢P�����Ƿ����t��ʹ����λ��������A��B��P�䡢C�������ɵĶ���ε��ܳ���̣������ڣ���t��ֵ��˵��������ƽ�Ƶķ����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������仭ͼ��
��1������AOB��120����
��2������AOB�Ľ�ƽ����OC��
��3�������ӳ�OC������OD��
��4���ֱ�������OA��OB��OD�ϻ��߶�OE��OF��OG��2cm��
��5������EF��EG��FG��
��6�����ܷ���EF��EG��FG��ʲô��ϵ����EFG����EGF����GEF��ʲô��ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���̴�λ���ҹ��������ˣ����㷢���ң���60��ʱ��ɵġ�ֱָ�㷨���ڡ��Ƕ����Ŵ���ѧ�����������˴�ͳ���������ȷ���������÷����������������⣺һ����ͷһ��ɮ����ɮ������������Сɮ���˷�һ������С���еü�������˼�ǣ���100�����з�100����ͷ����������1�˷�3����С����3�˷�1�������÷��꣬��С���и��ж����ˣ���С������__________�ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
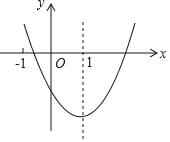
����Ŀ�����κ��� y=ax2+bx+c��a��0����ͼ����ͼ��ʾ���Գ�����ֱ�� x=1�����н��ۣ���ab��0����b2��4ac����a+b+2c��0����3a+c��0.������ȷ����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
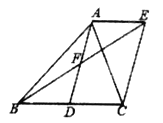
����Ŀ����ͼ��AD����ABC�����ߣ�AE��BC��BE��AD�ڵ�F����AF=DF.
(1)��֤:��AFE��ODFB��
(2)��֤:�ı���ADCE��ƽ���ı��Σ�
(3)��AB��AC֮������ʲô����ʱ���ı���ADCE�Ǿ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A. B���ع��ֱ���ƻ��30�ֺ�40�֣�C. D���ص�ũó�г��ֱ�����ƻ��20�ֺ�50�֡���֪��A. B���ص�C. D���ص��˼������
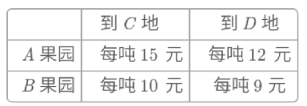
(1)��գ�����A���˵�C�ص�ƻ��Ϊ10�֣����A���˵�D�ص�ƻ��Ϊ___�֣���B���˵�C�ص�ƻ��Ϊ___�֣���B���˵�D�ص�ƻ��Ϊ___�֣��������Ϊ___Ԫ��
(2)����������Ϊ750Ԫʱ����ô��A���˵�C�ص�ƻ��Ϊ���ٶ�?
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com