
【题目】如图,直线AB,CD相交于点O,OA是∠EOC的平分线,∠EOD=100°.
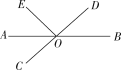
(1)请指出∠BOC的一个补角;
(2)求出∠BOD的度数.
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点.将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.
 试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有三个点A,B,C,回答下列问题:
(1)若将点B向右移动6个单位后,三个点所表示的数中最小的数是多少?
(2)在数轴上找一点D,使点D到A,C两点的距离相等,写出点D表示的数;
(3)在点B左侧找一点E,使点E到点A的距离是到点B的距离的2倍,并写出点E表示的数.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解黔东南州某县2013届中考学生的体育考试得分情况,从该县参加体育考试的4000名学生中随机抽取了100名学生的体育考试成绩作样本分析,得出如下不完整的频数统计表和频数分布直方图.
成绩分组 | 组中值 | 频数 |
25≤x<30 | 27.5 | 4 |
30≤x<35 | 32.5 | m |
35≤x<40 | 37.5 | 24 |
40≤x<45 | a | 36 |
45≤x<50 | 47.5 | n |
50≤x<55 | 52.5 | 4 |
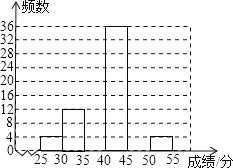
(1)求a、m、n的值,并补全频数分布直方图;
(2)若体育得分在40分以上(包括40分)为优秀,请问该县中考体育成绩优秀学生人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过解方程(组)使问题得到解决的思维方式就是方程思想,已学过的《勾股定理》及《一次函数》都与它有密切的联系,最近方程家族的《一元二次方程》我们也学习了它的求解方法和应用。如图1,矩形![]() 中,
中,![]() 在
在![]() 上,且
上,且![]() ,点
,点![]() 从点
从点![]() 出发,以1个单位每秒的速度在
出发,以1个单位每秒的速度在![]() 边上向点
边上向点![]() 运动,设点
运动,设点![]() 的运动时间为
的运动时间为![]() 秒。
秒。
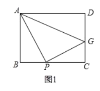
(1)![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并求出
的函数关系式,并求出![]() 时
时![]() 的值;
的值;
(2)在点![]() 从点
从点![]() 向
向![]() 运动的过程中,是否存在使
运动的过程中,是否存在使![]() 的时刻?若存在,求出
的时刻?若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
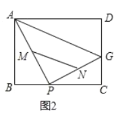
(3)如图2,![]() 分别是
分别是![]() 的中点,在点
的中点,在点![]() 从
从![]() 向
向![]() 运动的过程中,线段
运动的过程中,线段![]() 扫过的图形是什么形状_________________,并直接写出它的面积___________________________。
扫过的图形是什么形状_________________,并直接写出它的面积___________________________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,DC=5cm,在DC上存在一点E,沿直线AE把△AED折叠,使点D恰好落在BC边上,设此点为F,若△ABF的面积为30cm2,那么折叠△AED的面积为( )cm2
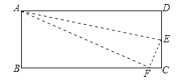
A. 16.9B. 14.4C. 13.5D. 11.8
查看答案和解析>>
科目:初中数学 来源: 题型:
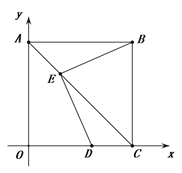
【题目】如图,在直角坐标系中,正方形ABCO的点B坐标(3,3),点A、C分别在y轴、x轴上,对角线AC上一动点E,连接BE,过E作DE⊥BE交OC于点D.若点D坐标为(2,0),则点E坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
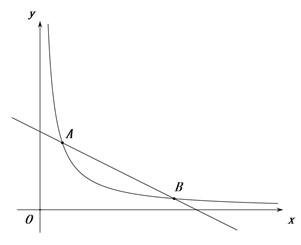
【题目】如图,一次函数y=-![]() x+b与反比例函数y=
x+b与反比例函数y=![]() (x>0)的图象交于点A(2,6)和B(m,1)
(x>0)的图象交于点A(2,6)和B(m,1)
(1)填空:一次函数的解析式为 ,反比例函数的解析式为 ;
(2)点E为y轴上一个动点,若S△AEB=5,求点E的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com