
【题目】如图,在长方形ABCD中,DC=5cm,在DC上存在一点E,沿直线AE把△AED折叠,使点D恰好落在BC边上,设此点为F,若△ABF的面积为30cm2,那么折叠△AED的面积为( )cm2
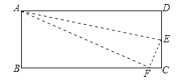
A. 16.9B. 14.4C. 13.5D. 11.8
【答案】A
【解析】
根据矩形的性质及三角形的面积公式求得BF=12cm,在Rt△ABF中,由勾股定理可得,AF=13cm;由折叠的性质可得AD=AF,DE=EF,设DE=xcm,则EC=(5-x)cm,EF=xcm,FC =1cm.在Rt△ECF中,由勾股定理可得方程(5-x)2 +12 =x2 ,解方程求得x的值,再由三角形的面积公式即可求得△AED的面积.
∵四边形ABCD是矩形,
∴∠B=∠C=90°,AB=CD=5cm,BC=AD,
∵△ABF的面积为30cm2,
∴BF=12cm,
在Rt△ABF中,由勾股定理可得,AF=![]() (cm);
(cm);
由折叠的性质可得AD=AF,DE=EF,
∴BC=AD=13cm,
设DE=xcm,则EC=(5-x)cm,EF=xcm,FC=BC-BF=13-12=1(cm).
在Rt△ECF中,由勾股定理可得,(5-x)2 +12 =x2 ,
解得x=![]() ,
,
即DE=![]() cm,
cm,
∴△AED的面积为:![]() AD×DE=
AD×DE=![]() (cm2)
(cm2)
故选A.


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】某批彩色弹力球的质量检验结果如下表:
抽取的彩色弹力球数n | 500 | 1000 | 1500 | 2000 | 2500 |
优等品频数m | 471 | 946 | 1426 | 1898 | 2370 |
优等品频率 | 0.942 | 0.946 | 0.951 | 0.949 | 0.948 |
(1)请在图中完成这批彩色弹力球“优等品”频率的折线统计图
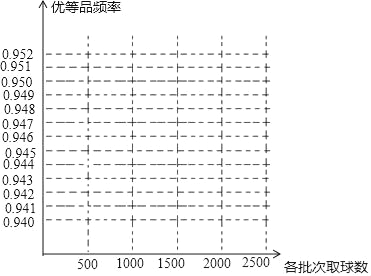
(2)这批彩色弹力球“优等品”概率的估计值大约是多少?(精确到0.01)
(3)从这批彩色弹力球中选择5个黄球、13个黑球、22个红球,它们除了颜色外都相同,将它们放入一个不透明的袋子中,求从袋子中摸出一个球是黄球的概率.
(4)现从第(3)问所说的袋子中取出若干个黑球,并放入相同数量的黄球,搅拌均匀,使从袋子中摸出一个黄球的概率为![]() ,求取出了多少个黑球?
,求取出了多少个黑球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们用a表示不大于 a 的最大整数,用 a 表示大于 a 的最小整数.例如:2.5 2 ,3 3 , 2.5 3 ;<2.5> 3 ,<4> 5 ,< 1.5> 1 .解决下列问题:
(1) 4.5 ,< 3.5> .
(2)若x 2 ,则 < x> 的取值范围是 ;若< y > 1,则 y 的取值范围是 .
(3)已知 x, y 满足方程组![]() ;求 x, y 的取值范围.
;求 x, y 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
一般地,在数轴上点![]() ,
,![]() 表示的实数分别为
表示的实数分别为![]() ,
,![]() (
(![]() ),则
),则![]() ,
,![]() 两点的距离
两点的距离![]() .如图,在数轴上点
.如图,在数轴上点![]() ,
,![]() 表示的实数分别为-3,4,则记
表示的实数分别为-3,4,则记![]() ,
,![]() ,因为
,因为![]() ,显然
,显然![]() ,
,![]() 两点的距离
两点的距离![]() .
.
若点![]() 为线段
为线段![]() 的中点,则
的中点,则![]() ,所以
,所以![]() ,即
,即![]() .
.
解决问题:
(1)直接写出线段![]() 的中点
的中点![]() 表示的实数
表示的实数![]() ;
;
(2)在点![]() 右侧的数轴上有点
右侧的数轴上有点![]() ,且
,且![]() ,求点
,求点![]() 表示的实数
表示的实数![]() ;
;
(3)在(2)的条件下,点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 的中点,若
的中点,若![]() ,
,![]() 两点同时沿数轴向正方向运动,
两点同时沿数轴向正方向运动,![]() 点的速度是
点的速度是![]() 点速度的2倍,
点速度的2倍,![]() 的中点
的中点![]() 和
和![]() 的中点
的中点![]() 也随之运动,3秒后,
也随之运动,3秒后,![]() ,则点
,则点![]() 的速度为每秒 个单位长度.
的速度为每秒 个单位长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.当轿车到达乙地后,马上沿原路以CD段速度返回,则货车从甲地出发_______小时后与轿车相遇(结果精确到0.01)
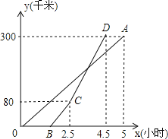
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() 为数轴上的两个点,点
为数轴上的两个点,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() .
.

(1)现有一只电子蚂蚁![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度向左运动,同时另一只电子蚂蚁
个单位长度的速度向左运动,同时另一只电子蚂蚁![]() 恰好从点
恰好从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度向右运动,设两只电子蚂蚁在数轴上的点
个单位长度的速度向右运动,设两只电子蚂蚁在数轴上的点![]() 处相遇,求点
处相遇,求点![]() 表示的数;
表示的数;
(2)若电子蚂蚁![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度向左运动,同时另一电子蚂蚁
个单位长度的速度向左运动,同时另一电子蚂蚁![]() 恰好从点
恰好从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度向左运动,设两只电子蚂蚁在数轴上的点
个单位长度的速度向左运动,设两只电子蚂蚁在数轴上的点![]() 处相遇,求点
处相遇,求点![]() 表示的数.
表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
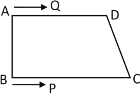
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=8cm,BC=10cm,AB=6cm,点Q从点A出发以1 cm/s的速度向点D运动,点P从点B出发以2 cm/s的速度向点C运动,P,Q两点同时出发,当点P到达点C时,两点同时停止运动.若设运动时间为t(s)
(1)直接写出:QD=______cm,PC=_______cm;(用含t的式子表示)
(2)当t为何值时,四边形PQDC为平行四边形?
(3)若点P与点C不重合,且DQ≠DP,当t为何值时,△DPQ是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)化简求值:(2+a)(2-a)+a(a-2b)+3a5b÷(-a2b)4,其中ab=-![]() .
.
(2)因式分解:a(n-1)2-2a(n-1)+a.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com