
����Ŀ��ͨ���ⷽ�̣��飩ʹ����õ������˼ά��ʽ���Ƿ���˼�룬��ѧ���ġ����ɶ���������һ�κ����������������е���ϵ��������̼���ġ�һԪ���η��̡�����Ҳѧϰ��������ⷽ����Ӧ�á���ͼ1������![]() �У�
��![]() ��
��![]() �ϣ���
�ϣ���![]() ����
����![]() �ӵ�
�ӵ�![]() ��������1����λÿ����ٶ���
��������1����λÿ����ٶ���![]() �������
�������![]() �˶������
�˶������![]() ���˶�ʱ��Ϊ
���˶�ʱ��Ϊ![]() �롣
�롣
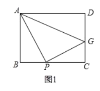
��1��![]() �����Ϊ
�����Ϊ![]() ����
����![]() ����
����![]() �ĺ�����ϵʽ�������
�ĺ�����ϵʽ�������![]() ʱ
ʱ![]() ��ֵ��
��ֵ��
��2���ڵ�![]() �ӵ�
�ӵ�![]() ��
��![]() �˶��Ĺ����У��Ƿ����ʹ
�˶��Ĺ����У��Ƿ����ʹ![]() ��ʱ�̣������ڣ����
��ʱ�̣������ڣ����![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
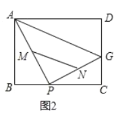
��3����ͼ2��![]() �ֱ���
�ֱ���![]() ���е㣬�ڵ�
���е㣬�ڵ�![]() ��
��![]() ��
��![]() �˶��Ĺ����У��߶�
�˶��Ĺ����У��߶�![]() ɨ����ͼ����ʲô��״_________________����ֱ��д���������___________________________��
ɨ����ͼ����ʲô��״_________________����ֱ��д���������___________________________��
���𰸡���1��x=8����2�����ڣ�x=6����3��ƽ���ı��Σ�15.
��������
��1��![]() ��
��![]() ��Ȼ������
��Ȼ������![]() �����
�����![]() ������
���ε����![]() ����ֱ�������ε�����ɵõ�
����ֱ�������ε�����ɵõ�![]() ��
��![]() �ĺ�����ϵʽ��Ȼ��
�ĺ�����ϵʽ��Ȼ��![]() ���뺯����ϵʽ�����
���뺯����ϵʽ�����![]() ��ֵ��
��ֵ��
��2�������ݹ��ɶ������![]() ��
��![]() ��
��![]() �ij���Ȼ�����ݹ��ɶ������涨���г�����
�ij���Ȼ�����ݹ��ɶ������涨���г�����![]() �ķ��̣��Ӷ������
�ķ��̣��Ӷ������![]() ��ֵ��
��ֵ��
��3��ȷ������![]() �ֱ����
�ֱ����![]() �͵�
�͵�![]() �غ�ʱ����
�غ�ʱ����![]() ��
��![]() ��λ�ã�Ȼ�����������ε���λ�߶�����֤��
��λ�ã�Ȼ�����������ε���λ�߶�����֤��![]() ��
��![]() ���Ӷ����жϳ�
���Ӷ����жϳ�![]() ɨ���������״��Ȼ������ƽ���ı��ε������ʽ��⼴�ɣ�
ɨ���������״��Ȼ������ƽ���ı��ε������ʽ��⼴�ɣ�
�⣺��1��![]() �ı���
�ı���![]() Ϊ���Σ�
����
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
�����ã�![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
��ã�![]() ��
��
��2�����ڣ��������£�
![]() ��
��![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() ʱ��
ʱ��![]() ��
��
![]() ��
��
�����ã�![]() ��
��
�䷽�ã�![]() ��
��
��ã�![]() ��
��
��3����ͼ��ʾ��
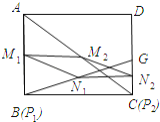
![]() ����
����![]() ���
���![]() �غ�ʱ����
�غ�ʱ����![]() λ��
�![]() ������
������![]() λ�ڵ�
λ�ڵ�![]() ����
����
![]() Ϊ
Ϊ![]() ���е㣬��
���е㣬��![]() λ
λ![]() ���е㣮
���е㣮
![]() ����
����![]() ���
���![]() �غ�ʱ����
�غ�ʱ����![]() λ��
�![]() ������
������![]() λ�ڵ�
λ�ڵ�![]() ����
����
![]() Ϊ
Ϊ![]() ���е㣬��
���е㣬��![]() λ
λ![]() ���е㣮
���е㣮
![]() ��
��![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
![]() �ı���
�ı���![]() Ϊƽ���ı��Σ�
Ϊƽ���ı��Σ�
![]() ɨ��������Ϊƽ���ı��Σ�
ɨ��������Ϊƽ���ı��Σ�
![]()
�ʴ�Ϊ��ƽ���ı��Σ�15��


 ������ʱͬ����ϰ��ϵ�д�
������ʱͬ����ϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�İ뾶OD����AB�ڵ�C������BO���ӳ�����O�ڵ�E������AE����AB=6��CD=1����AE�ij�Ϊ��������
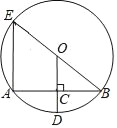
A. 3![]() B. 8 C. 12 D. 8
B. 8 C. 12 D. 8![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijʯ����ϩ��ij���������ס����������ϵ������Ϣ���±����������������⣺
������ | �ɱ��� | ���۴����� | |
�������� | 2100��Ԫ/�֣� | 800��Ԫ/�֣� | 200��Ԫ/�֣� |
�������� | 2400��Ԫ/�֣� | 1100��Ԫ/�֣� | 100��Ԫ/�֣� ��ÿ�»���֧���豸������ά����20000Ԫ |
��1����ó���ÿ�������ס����������ϸ�x�֣�����ֱ�Ϊy1Ԫ��y2Ԫ���ֱ����y1��y2��x�ĺ�����ϵʽ(ע������=������-��֧��)��
��2����֪�ó���ÿ�������ס����������Ͼ�������400�֣���ij��Ҫ�����ס����������Ϲ�700�֣�����������ס������ϸ����ٶ�ʱ����õ������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ��������
������ͼ��
���壺��ij��ͼ�οɷָ�Ϊ���ɸ����������Ƶ�ͼ�Σ�������ͼ����������ͼ�Σ����磺������ABCD�У���E��F��G��H�ֱ���AB��BC��CD��DA�ߵ��е㣬����EG��HF���ڵ�O����֪�ָ�ɵ��ĸ��ı���AEOH��EBFO��OFCG��HOGD��Ϊ�����Σ�����ԭ���������ƣ�����������������ͼ�Σ�
����
��1��ͼ1��������ABCD�ָ�ɵ��ĸ�С�������У�ÿ����������ԭ�����ε����Ʊ�Ϊ�� ����
��2����ͼ2����֪��ABC�У���ACB=90�㣬AC=4��BC=3��С��������ABCҲ�ǡ�������ͼ�Ρ�������˼·�ǣ�����C��CD��AB�ڵ�D����CD����ABC�ָ��2�������Լ����Ƶ�Сֱ�������Σ���֪��ACD�ס�ABC������ACD����ABC�����Ʊ�Ϊ�� ����
��3������һ������ABCD��������ͼ�Σ����г�AD=a����AB=b��a��b����
�������A��B��������ѡһ��������ѡ���� ���⣮
A������ͼ3��1����������ABCD����ָ������ȫ�Ⱦ��Σ�����ԭ���ζ����ƣ���a=�� �����ú�b��ʽ�ӱ�ʾ����
����ͼ3��2��������ABCD����ָ��n��ȫ�Ⱦ��Σ�����ԭ���ζ����ƣ���a=�� �����ú�n��b��ʽ�ӱ�ʾ����
B������ͼ4��1����������ABCD������ָ��2��ȫ�Ⱦ��Σ��ٽ�ʣ��IJ��ֺ���ָ��3��ȫ�Ⱦ��Σ��ҷָ�õ��ľ�����ԭ���ζ����ƣ���a=�� �����ú�b��ʽ�ӱ�ʾ����
����ͼ4��2����������ABCD������ָ��m��ȫ�Ⱦ��Σ��ٽ�ʣ��IJ��ֺ���ָ��n��ȫ�Ⱦ��Σ��ҷָ�õ��ľ�����ԭ���ζ����ƣ���a=�� �����ú�m��n��b��ʽ�ӱ�ʾ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����¥AB�ĸ�Ϊ16m��Զ����һ��CD��С����¥��A���������D��������Ϊ 60�㣬��¥��B���������D��������Ϊ45�㣬����A��C����ֱ�λ��B��D�������·�����A��C������ͬһˮƽ���ϣ�����CD�ĸߣ���![]() =1.73���������һλС������
=1.73���������һλС������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��CD�ཻ�ڵ�O��OA�ǡ�EOC��ƽ���ߣ���EOD��100����
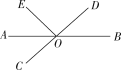
(1)��ָ����BOC��һ�����ǣ�
(2)�����BOD�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����3���ڵ���ʳ������Ķ���Ϊ��+26��-32��-15��+34��-38��-20���ʣ�
��1��������3�죬�������ʳ�������˶��٣����Ǽ����˶��٣�
��2��������3�죬�ֿ����Ա���ֿ��ﻹ����520����ʳ����ô3��ǰ����������ٶ֣�
��3�����������װж�Ѷ���ÿ��5Ԫ����ô��3����Ҫ����װж�ѣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ij��2017����ҵ��ˮ��x���֣������Ӧ����ˮ��y��Ԫ��֮��ĺ�����ϵ��ͼ��ʾ��
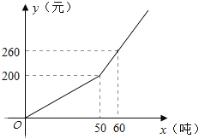
��1����y����x�ĺ�����ϵʽ��
��2����ij��ҵ2017��10�·ݵ�ˮ��Ϊ620Ԫ�������ҵ2017��10�·ݵ���ˮ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
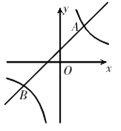
����Ŀ����ͼ��һ�κ��� y=k x+b �뷴�������� ![]() ͼ���ڵ� A (2��m) �͵� B��n��-2��.
ͼ���ڵ� A (2��m) �͵� B��n��-2��.
��1�� ���һ�κ�������ʽ��m��n��ֵ��
��2�� ���ͼ����ʽ![]() �Ľ⼯.
�Ľ⼯.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com