练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

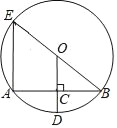
    【题目】如图，⊙O的半径OD⊥弦AB于点C，连接BO并延长交⊙O于点E，连接AE，若AB=6，CD=1，则AE的长为（　　）

    A. 3 B. 8 C. 12 D. 8

    【答案】B

    【解析】分析：设⊙O的半径为R，由OD⊥AB，根据垂径定理得AC=BC=AB=3，在Rt△AOC中，OA=R，OC=R-CD=R-1，根据勾股定理得到（R-1）2+32=R2，解得R=5，则OC=1，由于OC为△ABE的中位线，即可求出AE的长度．

    详解：设⊙O的半径为R，如图，

    ∵OD⊥AB，

    ∴AC=BC=AB=×6=3，

    在Rt△AOC中，OA=R，OC=R-CD=R-1，

    ∵OC2+AC2=OA2，

    ∴（R-1）2+32=R2，解得R=5，

    ∴OC=5-1=4，

    ∴AE=2OC=8，

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知：在四边形ABCD中，∠ABC=∠ADC=90，M、N分别是CD和BC上的点．

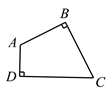
    求作：点M、N，使△AMN的周长最小．

    作法：如图，

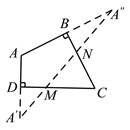
    （1）延长AD，在AD的延长线上截取DA=DA；

    （2）延长AB，在AB的延长线上截取B A″=BA；

    （3）连接A′A″，分别交CD、BC于点M、N．则点M、N即为所求作的点．

    请回答：这种作法的依据是_____________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某物流公司的快递车和货车每天沿同一条路线往返于A、B两地，快递车比货车多往返一趟．如图所示，表示货车距离A地的路程y（单位：h）与所用时间x（单位h）的图像，其间在B地装卸货物2h．已知快递车比货车早1h出发，最后一次返回A地比货车晚1h．若快递车往返途中速度不变，且在A、B两地均不停留，则两车在往返途中相遇的次数为________次．

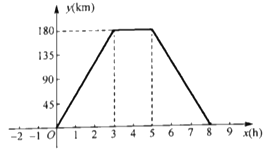
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形纸片ABCD中，∠B=∠D=90°，点E，F分别在边BC，CD上，将AB，AD分别沿AE，AF折叠，点B，D恰好都和点G重合，∠EAF=45°．

    （1）求证：四边形ABCD是正方形；

    （2）求证：三角形ECF的周长是四边形ABCD周长的一半；

    （3）若EC=FC=1，求AB的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】以正方形ABCD的边AD作等边△ADE，则∠BEC的度数是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠BAC=90°，AC=2AB，点D是AC的中点．将一块锐角为45°的直角三角板如图放置，使三角板斜边的两个端点分别与A、D重合，连接BE、EC．

    试猜想线段BE和EC的数量及位置关系，并证明你的猜想．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，在正方形ABCD中，点E与点F分别在线段AC、BC上，且四边形DEFG是正方形．

    （1）试探究线段AE与CG的关系，并说明理由．

    （2）如图②若将条件中的四边形ABCD与四边形DEFG由正方形改为矩形，AB=3，BC=4．

    ①线段AE、CG在（1）中的关系仍然成立吗？若成立，请证明，若不成立，请写出你认为正确的关系，并说明理由．

    ②当△CDE为等腰三角形时，求CG的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，△ABC是边长为2的等边三角形，D是AB边的中点，F是BC边上的动点，E是AC边上的动点，当E、F的位置在何处时，才能使的周长最小？简要说明作法．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

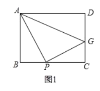
    【题目】通过解方程（组）使问题得到解决的思维方式就是方程思想，已学过的《勾股定理》及《一次函数》都与它有密切的联系，最近方程家族的《一元二次方程》我们也学习了它的求解方法和应用。如图1，矩形中，在上，且，点从点出发，以1个单位每秒的速度在边上向点运动，设点的运动时间为秒。

    （1）的面积为，求关于的函数关系式，并求出时的值；

    （2）在点从点向运动的过程中，是否存在使的时刻？若存在，求出的值，若不存在，请说明理由；

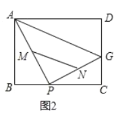
    （3）如图2，分别是的中点，在点从向运动的过程中，线段扫过的图形是什么形状_________________，并直接写出它的面积___________________________。

    查看答案和解析>>

    同步练习册答案