
【题目】如图所示,△ABC是边长为2的等边三角形,D是AB边的中点,F是BC边上的动点,E是AC边上的动点,当E、F的位置在何处时,才能使![]() 的周长最小?简要说明作法.
的周长最小?简要说明作法.

【答案】点E、F分别为AC、BC中点时,△DEF的周长最小.
【解析】
分别作点D关于BC、AC的对称点D1、D2,交AC、BC于M、N,连接![]() ,分别交AC、BC于点E、F,根据轴对称的性质可得DE=D1E,DF=D2F,DM⊥AC,DN⊥BC,DM=D1M,DN=D2N,D1D2是△DEF的最小值,由等边三角形的性质可得∠B=∠A=60°,可得∠ADM=∠BDN=30°,即可得∠D1DD2=120°,利用ASA可证明△ADM≌△BDN,可得DD2=DD1,根据等腰三角形的性质可得∠D1=∠D2=30°,即可证明∠D1=∠ADM,利用ASA可证明△ADM≌△ED1M,可得AM=EM,可证明AD=AE,即可证明点E为AC的中点,同理可得点F为BC的中点,可得答案.
,分别交AC、BC于点E、F,根据轴对称的性质可得DE=D1E,DF=D2F,DM⊥AC,DN⊥BC,DM=D1M,DN=D2N,D1D2是△DEF的最小值,由等边三角形的性质可得∠B=∠A=60°,可得∠ADM=∠BDN=30°,即可得∠D1DD2=120°,利用ASA可证明△ADM≌△BDN,可得DD2=DD1,根据等腰三角形的性质可得∠D1=∠D2=30°,即可证明∠D1=∠ADM,利用ASA可证明△ADM≌△ED1M,可得AM=EM,可证明AD=AE,即可证明点E为AC的中点,同理可得点F为BC的中点,可得答案.
如图所示,作点D关于AC的对称点D1,作点D关于BC的对称点![]() ,交AC、BC于M、N,连接
,交AC、BC于M、N,连接![]() ,分别交AC、BC于点E、F,
,分别交AC、BC于点E、F,
∴DE=D1E,DF=D2F,DM⊥AC,DN⊥BC,DM=D1M,DN=D2N,
∴DE+DF+EF=D1E+EF+D2F=D1D2,
∴D1D2即是△DEF的最小值,则点E、F即为所求,
∵△ABC是等边三角形,
∴∠A=∠B=60°,
∴∠ADM=∠BDN=90°-60°=30°,
∴∠D1DD2=180°-30°-30°=120°,
∵点D为AB中点,
∴AD=BD,
在△BDN和△ADM中,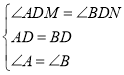 ,
,
∴△ADM≌△BDN,
∴DN=DM,
∴DD2=DD1,
∴∠D1=∠D2=30°,
∴∠D1=∠ADM,
在△ADM和△ED1M中,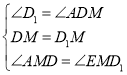 ,
,
∴△ADM≌△ED1M,
∴AM=EM,
∵∠ADM=30°,DM⊥AC,
∴AM=![]() AD,
AD,
∴AE=AD,
∴点E为AC中点,
同理可得:点F为BC中点,
∴点E、F分别为AC、BC中点时,△DEF的周长最小.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,F为CD上一点,∠EFD=60°,∠AEC=2∠CEF,若6°<∠BAE<15°,∠C的度数为整数,则∠C的度数为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径OD⊥弦AB于点C,连接BO并延长交⊙O于点E,连接AE,若AB=6,CD=1,则AE的长为( )
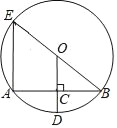
A. 3![]() B. 8 C. 12 D. 8
B. 8 C. 12 D. 8![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图l,在四边形ABCD中.∠DAB被对角线AC平分,且AC2=AB·AD,我们称该四边形为“可分四边形”∠DAB称为“可分角”.

(1)如图2,四边形ABCD为“可分四边形”,∠DAB为“可分角”,求证:△DAC∽△CAB.
(2)如图2,四边形ABCD为“可分四边形”,∠DAB为“可分角”,如果∠DCB=∠DAB 则∠DAB = .
(3)现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4.BC=2.∠D=90°,则AD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2、C2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某石化乙烯厂某车间生产甲、乙两种塑料的相关信息如下表,请你解答下列问题:
出厂价 | 成本价 | 排污处理费 | |
甲种塑料 | 2100(元/吨) | 800(元/吨) | 200(元/吨) |
乙种塑料 | 2400(元/吨) | 1100(元/吨) | 100(元/吨) 另每月还需支付设备管理、维护费20000元 |
(1)设该车间每月生产甲、乙两种塑料各x吨,利润分别为y1元和y2元,分别求出y1和y2与x的函数关系式(注:利润=总收入-总支出);
(2)已知该车间每月生产甲、乙两种塑料均不超过400吨,若某月要生产甲、乙两种塑料共700吨,求该月生产甲、乙塑料各多少吨时,获得的总利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成任务:
自相似图形
定义:若某个图形可分割为若干个都与它相似的图形,则称这个图形是自相似图形.例如:正方形ABCD中,点E、F、G、H分别是AB、BC、CD、DA边的中点,连接EG,HF交于点O,易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形,且与原正方形相似,故正方形是自相似图形.
任务:
(1)图1中正方形ABCD分割成的四个小正方形中,每个正方形与原正方形的相似比为 ;
(2)如图2,已知△ABC中,∠ACB=90°,AC=4,BC=3,小明发现△ABC也是“自相似图形”,他的思路是:过点C作CD⊥AB于点D,则CD将△ABC分割成2个与它自己相似的小直角三角形.已知△ACD∽△ABC,则△ACD与△ABC的相似比为 ;
(3)现有一个矩形ABCD是自相似图形,其中长AD=a,宽AB=b(a>b).
请从下列A、B两题中任选一条作答:我选择 题.
A:①如图3﹣1,若将矩形ABCD纵向分割成两个全等矩形,且与原矩形都相似,则a= (用含b的式子表示);
②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形,且与原矩形都相似,则a= (用含n,b的式子表示);
B:①如图4﹣1,若将矩形ABCD先纵向分割出2个全等矩形,再将剩余的部分横向分割成3个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含b的式子表示);
②如图4﹣2,若将矩形ABCD先纵向分割出m个全等矩形,再将剩余的部分横向分割成n个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含m,n,b的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某市2017年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图所示.
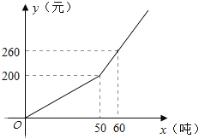
(1)求y关于x的函数关系式;
(2)若某企业2017年10月份的水费为620元,求该企业2017年10月份的用水量;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com