
【题目】如图,在四边形纸片ABCD中,∠B=∠D=90°,点E,F分别在边BC,CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都和点G重合,∠EAF=45°.
(1)求证:四边形ABCD是正方形;
(2)求证:三角形ECF的周长是四边形ABCD周长的一半;
(3)若EC=FC=1,求AB的长度.

【答案】(1)见解析;(2)见解析;(3)![]() +1
+1
【解析】分析:(1)由题意得,∠BAE=∠EAG,∠DAF=∠FAG,于是得到∠BAD=2∠EAF=90°,推出四边形ABCD是矩形,根据正方形的判定定理即可得到结论;
(2)根据EG=BE,FG=DF,得到EF=BE+DF,于是得到△ECF的周长=EF+CE+CF=BE+DF+CE+CF=BC+CD,即可得到结论;
(3)根据EC=FC=1,得到BE=DF,根据勾股定理得到EF=![]() ,于是得到结论.
,于是得到结论.
详(1)证明:由题意得,∠BAE=∠EAG,∠DAF=∠FAG,
∴∠BAD=2∠EAF=90°,
∴四边形ABCD是矩形,
∵AB=AG,AD=AG,
∴AB=AD,
∴四边形ABCD是正方形;
(2)证明:∵EG=BE,FG=DF,
∴EF=BE+DF,
∴△ECF的周长=EF+CE+CF=BE+DF+CE+CF=BC+CD,
∴三角形ECF的周长是四边形ABCD周长的一半;
(3)∵EC=FC=1,
∴BE=DF,
∴EF=![]() ,
,
∵EF=BE+DF,
∴BE=DF=![]() EF=
EF=![]() ,
,
∴AB=BC=BE+EC=![]() +1.
+1.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校假期由校长带领该校“三好学生”去旅游,甲旅行社说“若校长买全票一张,则学生半价.”乙旅行社说“全部人六折优惠”若全票价是1200元,则:
(1)若学生人数是20人,甲、乙旅行社收费分别是多少?
(2)当学生人数的多少时,两家旅行社的收费一样?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句正确的个数是( )
①收入增加100元与支出减少200元是一对具有相反意义的量;
②数轴上原点两侧的数互为相反数;
③若一个数小于他的绝对值,则这个数是负数;
④若a、b互为相反数,则![]() 与
与![]() 也互为相反数
也互为相反数
A.1个B.2个C.3个D.0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察与思考:阅读下列材料,并解决后面的问题
在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,过A作AD⊥BC于D(如图(1)),则![]() ,即AD=csinB,AD=bsinC,于是csinB=bsinC,即
,即AD=csinB,AD=bsinC,于是csinB=bsinC,即![]() ,同理有:
,同理有: ![]() ,所以
,所以![]() .
.
即:在一个锐角三角形中,各边和它所对角的正弦的比相等在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论和有关定理就可以求出其余三个未知元素.
根据上述材料,完成下列各题.

(1)如图(2),△ABC中,∠B=45°,∠C=75°,BC=60,则∠A= ;AC= ;
(2)某次巡逻中,如图(3),我渔政船在C处测得钓鱼岛A在我渔政船的北偏西30°的方向上,随后以40海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得钓鱼岛A在的北偏西75°的方向上,求此时渔政船距钓鱼岛A的距离AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017山东省莱芜市)如图,正五边形ABCDE的边长为2,连结AC、AD、BE,BE分别与AC和AD相交于点F、G,连结DF,给出下列结论:①∠FDG=18°;②FG=3﹣![]() ;③(S四边形CDEF)2=9+2
;③(S四边形CDEF)2=9+2![]() ;④DF2﹣DG2=7﹣2
;④DF2﹣DG2=7﹣2![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
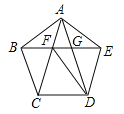
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
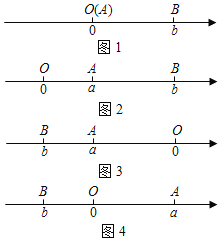
点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为|AB|
当A、B两点中有一点在原点时,不妨设点A在原点(如图1)|AB|=|OB|=|b|=|a﹣b|;
当A、B两点都不在原点时
①当点A、B都在原点的右边(如图2)
|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|
②当点A、B都在原点的左边(如图3)
|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=|a﹣b|
③当点A、B在原点的两边(如图4)
|AB|=|OB|+|OA|=|b|+|a|=﹣b+a=|a﹣b|
回答下列问题:
(1)数轴上表示1和5的两点之间的距离是 ,数轴上表示1和﹣3的两点之间的距离是 ;
(2)数轴上若点A表示的数是x,点B表示的数是﹣2,则点A和B之间的距离是 ,若|AB|=3,那么x为 ;
(3)当x是 时,代数式|x+2|+|x﹣1|=5;
(4)若点A表示的数﹣1,点B与点A的距离是10,且点B在点A的右侧,动点P、Q同时从A、B出发沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒![]() 个单位长度,求运动几秒后,点Q与点P相距1个单位?(请写出必要的求解过程)
个单位长度,求运动几秒后,点Q与点P相距1个单位?(请写出必要的求解过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
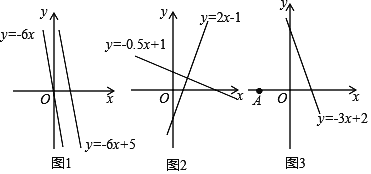
【题目】材料一:如图1,由课本91页例2画函数y=﹣6x与y=﹣6x+5可知,直线y=﹣6x+5可以由直线y=﹣6x向上平移5个单位长度得到由此我们得到正确的结论一:在直线L1:y=K1x+b1与直线L2:y=K2x+b2中,如果K1=K2 且b1≠b2 ,那么L1∥L2,反过来,也成立.
材料二:如图2,由课本92页例3画函数y=2x﹣1与y=﹣0.5x+1可知,利用所学知识一定能证出这两条直线是互相垂直的.由此我们得到正确的结论二:在直线L1:y=k1x+b1 与L2:y=k2x+b2 中,如果k1·k2=-1那么L1⊥L2,反过来,也成立
应用举例
已知直线y=﹣![]() x+5与直线y=kx+2互相垂直,则﹣
x+5与直线y=kx+2互相垂直,则﹣![]() k=﹣1.所以k=6
k=﹣1.所以k=6
解决问题
(1)请写出一条直线解析式______,使它与直线y=x﹣3平行.
(2)如图3,点A坐标为(﹣1,0),点P是直线y=﹣3x+2上一动点,当点P运动到何位置时,线段PA的长度最小?并求出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明对自己上学路线的长度进行了20次测量,得到20个数据x1,x2,…,x20,已知x1+x2+…+x20=2019,当代数式(x﹣x1)2+(x﹣x2)2+…+(x﹣x20)2取得最小值时,x的值为___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com