
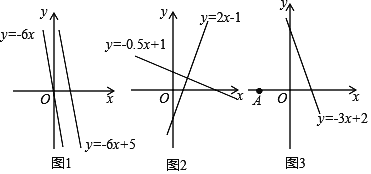
【题目】材料一:如图1,由课本91页例2画函数y=﹣6x与y=﹣6x+5可知,直线y=﹣6x+5可以由直线y=﹣6x向上平移5个单位长度得到由此我们得到正确的结论一:在直线L1:y=K1x+b1与直线L2:y=K2x+b2中,如果K1=K2 且b1≠b2 ,那么L1∥L2,反过来,也成立.
材料二:如图2,由课本92页例3画函数y=2x﹣1与y=﹣0.5x+1可知,利用所学知识一定能证出这两条直线是互相垂直的.由此我们得到正确的结论二:在直线L1:y=k1x+b1 与L2:y=k2x+b2 中,如果k1·k2=-1那么L1⊥L2,反过来,也成立
应用举例
已知直线y=﹣![]() x+5与直线y=kx+2互相垂直,则﹣
x+5与直线y=kx+2互相垂直,则﹣![]() k=﹣1.所以k=6
k=﹣1.所以k=6
解决问题
(1)请写出一条直线解析式______,使它与直线y=x﹣3平行.
(2)如图3,点A坐标为(﹣1,0),点P是直线y=﹣3x+2上一动点,当点P运动到何位置时,线段PA的长度最小?并求出此时点P的坐标.
【答案】(1)y=x;(2)当线段PA的长度最小时,点P的坐标为![]() .
.
【解析】
(1)由两直线平行可得出k1=k2=1、b1≠b2=﹣3,取b1=0即可得出结论;
(2)过点A作AP⊥直线y=﹣3x+2于点P,此时线段PA的长度最小,由两直线平行可设直线PA的解析式为y=![]() x+b,由点A的坐标利用待定系数法可求出直线PA的解析式,联立两直线解析式成方程组,再通过解方程组即可求出:当线段PA的长度最小时,点P的坐标.
x+b,由点A的坐标利用待定系数法可求出直线PA的解析式,联立两直线解析式成方程组,再通过解方程组即可求出:当线段PA的长度最小时,点P的坐标.
.解:(1)∵两直线平行,
∴k1=k2=1,b1≠b2=﹣3,
∴该直线可以为y=x.
故答案为:y=x.
(2)过点A作AP⊥直线y=﹣3x+2于点P,此时线段PA的长度最小,如图所示.
∵直线PA与直线y=﹣3x+2垂直,
∴设直线PA的解析式为y=![]() x+b.
x+b.
∵点A(﹣1,0)在直线PA上,
∴![]() ×(﹣1)+b=0,解得:b=
×(﹣1)+b=0,解得:b=![]() ,
,
∴直线PA的解析式为y=![]() x+
x+![]() .
.
联立两直线解析式成方程组,得:
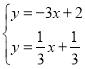 ,解得:
,解得:![]() .
.
∴当线段PA的长度最小时,点P的坐标为(![]() ,
,![]() ).
).



 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
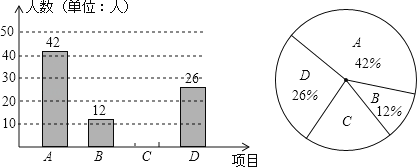
【题目】为开展“学生每天锻炼1小时”的活动,我市某中学根据学校实际情况,决定开设A:毽子,B:篮球,C:跑步,D:跳绳四种运动项目.为了了解学生最喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如图统计图.请结合图中信息解答下列问题:
(1)该校本次调查中,共调查了多少名学生?
(2)计算本次调查学生中喜欢“跑步”的人数和百分比,并请将两个统计图补充完整;
(3)在本次调查的学生中随机抽取1人,他喜欢“跑步”的概率有多大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图反映的过程是小明从家去菜地浇水,又去玉米地锄草,然后回家.其中x表示时间,y表示小明离他家的距离.根据图象回答下列问题:

①菜地离小明家多远?小明走到菜地用了多少时间?
②小明给菜地浇水用了多少时间?
③玉米地离菜地、小明家多远?小明从玉米地走回家平均速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形纸片ABCD中,∠B=∠D=90°,点E,F分别在边BC,CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都和点G重合,∠EAF=45°.
(1)求证:四边形ABCD是正方形;
(2)求证:三角形ECF的周长是四边形ABCD周长的一半;
(3)若EC=FC=1,求AB的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条直路上的![]() 、
、![]() 、
、![]() 、
、![]() 四个车站的位置如图所示(单位千米),如果小明家在
四个车站的位置如图所示(单位千米),如果小明家在![]() 站旁,他的同学小亮家在
站旁,他的同学小亮家在![]() 站旁,新华书店在
站旁,新华书店在![]() 站旁,一天小明乘车从
站旁,一天小明乘车从![]() 站出发到
站出发到![]() 站下车去新华书店购买一些课外阅读书籍,途径
站下车去新华书店购买一些课外阅读书籍,途径![]() 、
、![]() 两站,当小明到达
两站,当小明到达![]() 站时发现自己所带钱不够购买自己所要的书籍.于是他乘车返回到
站时发现自己所带钱不够购买自己所要的书籍.于是他乘车返回到![]() 站处下车向小亮借足了钱,然后乘车继续赶往
站处下车向小亮借足了钱,然后乘车继续赶往![]() 站旁的新华书店.
站旁的新华书店.
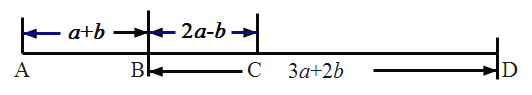
(1)求![]() 、
、![]() 两站的距离;(用含有
两站的距离;(用含有![]() 、
、![]() 的代数式表示)
的代数式表示)
(2)求这一天小明从![]() 站到
站到![]() 站乘车路程.(用含有
站乘车路程.(用含有![]() 、
、![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次将点A向左移动2个单位长度到达点![]() ,第二次将点
,第二次将点![]() 向右移动4个单位长度到达点
向右移动4个单位长度到达点![]() ,第三次将点
,第三次将点![]() 向左移动6个单位长度到达点
向左移动6个单位长度到达点![]() ,....按照这种移动规律进行下去;
,....按照这种移动规律进行下去;
(1)第9次移动到点![]() ,求点
,求点![]() 所表示的数;
所表示的数;
(2)第n次移动到点![]() ,如果点
,如果点![]() 表示的数是19,求n;
表示的数是19,求n;
(3)第n次移动到点![]() ,如果点
,如果点![]() 与原点的距离是99,求n。
与原点的距离是99,求n。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E、F分别是矩形ABCD的边AB、BC的中点,连AF,CE,AF、CE交于G,则四边形BEGF与四边形ADCG的面积的比值为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】浠水县商场某柜台销售每台进价分别为160元、120元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 4台 | 1200元 |
第二周 | 5台 | 6台 | 1900元 |
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若商场准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,商场销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△BAC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′,若∠CC′B′=30°,求∠B的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com