
【题目】在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次将点A向左移动2个单位长度到达点![]() ,第二次将点
,第二次将点![]() 向右移动4个单位长度到达点
向右移动4个单位长度到达点![]() ,第三次将点
,第三次将点![]() 向左移动6个单位长度到达点
向左移动6个单位长度到达点![]() ,....按照这种移动规律进行下去;
,....按照这种移动规律进行下去;
(1)第9次移动到点![]() ,求点
,求点![]() 所表示的数;
所表示的数;
(2)第n次移动到点![]() ,如果点
,如果点![]() 表示的数是19,求n;
表示的数是19,求n;
(3)第n次移动到点![]() ,如果点
,如果点![]() 与原点的距离是99,求n。
与原点的距离是99,求n。
【答案】(1)-9;(2)n=18;(3)n=98或99.
【解析】
根据题意依次得出点A移动的规律,当点A奇数次移动时,对应表示的数为负数,当点A偶数次移动时,对应表示的数为正数,得出对应规律:①当n为奇数时,第n次移动的点表示的数为:-n,②当n为偶数时,第n次移动的点表示的数为:n+1,(1)根据规律,可判断n=9时表示的数;(2)根据表示的数为正数,所以n为偶数,即可求出n;(3)根据点An与原点的距离等于99,则点An表示的数为99或-99,分别代入计算即可.
解:第一次:A1表示:12=1,
第二次:A2表示:1+4=3,
第三次:A3表示:36=3
第四次:A4表示:3+8=5,
…
当n为奇数时,第n次移动的点表示的数为:n,
当n为偶数时,第n次移动的点表示的数为:n+1,
(1)第9次移动时,![]() 所表示的数为-9;
所表示的数为-9;
(2)∵![]() 表示的数位19,
表示的数位19,
∴n为偶数,即n+1=19,
∴n=18;
(3)∵点An与原点的距离等于99,
∴点An表示的数为99或99,
∴n+1=99或n=99,
故n=98或99.


科目:初中数学 来源: 题型:
【题目】一家商店进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付两组费用共3520元,若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元,问:
(1)甲,乙两组工作一天,商店各应付多少钱?
(2)已知甲单独完成需12天,乙单独完成需24天,单独请哪个组,商店所需费用最少?
(3)若装修完后,商店每天可贏利200元,你认为如何安排施工更有利于商店?请你帮助商店决策.(可用(1)(2)问的条件及结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察与思考:阅读下列材料,并解决后面的问题
在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,过A作AD⊥BC于D(如图(1)),则![]() ,即AD=csinB,AD=bsinC,于是csinB=bsinC,即
,即AD=csinB,AD=bsinC,于是csinB=bsinC,即![]() ,同理有:
,同理有: ![]() ,所以
,所以![]() .
.
即:在一个锐角三角形中,各边和它所对角的正弦的比相等在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论和有关定理就可以求出其余三个未知元素.
根据上述材料,完成下列各题.

(1)如图(2),△ABC中,∠B=45°,∠C=75°,BC=60,则∠A= ;AC= ;
(2)某次巡逻中,如图(3),我渔政船在C处测得钓鱼岛A在我渔政船的北偏西30°的方向上,随后以40海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得钓鱼岛A在的北偏西75°的方向上,求此时渔政船距钓鱼岛A的距离AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为|AB|
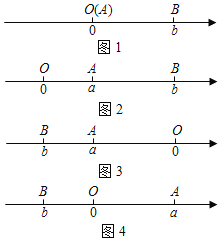
当A、B两点中有一点在原点时,不妨设点A在原点(如图1)|AB|=|OB|=|b|=|a﹣b|;
当A、B两点都不在原点时
①当点A、B都在原点的右边(如图2)
|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|
②当点A、B都在原点的左边(如图3)
|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=|a﹣b|
③当点A、B在原点的两边(如图4)
|AB|=|OB|+|OA|=|b|+|a|=﹣b+a=|a﹣b|
回答下列问题:
(1)数轴上表示1和5的两点之间的距离是 ,数轴上表示1和﹣3的两点之间的距离是 ;
(2)数轴上若点A表示的数是x,点B表示的数是﹣2,则点A和B之间的距离是 ,若|AB|=3,那么x为 ;
(3)当x是 时,代数式|x+2|+|x﹣1|=5;
(4)若点A表示的数﹣1,点B与点A的距离是10,且点B在点A的右侧,动点P、Q同时从A、B出发沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒![]() 个单位长度,求运动几秒后,点Q与点P相距1个单位?(请写出必要的求解过程)
个单位长度,求运动几秒后,点Q与点P相距1个单位?(请写出必要的求解过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
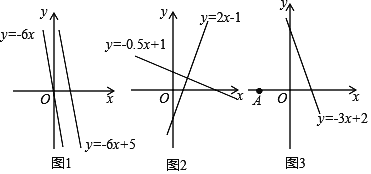
【题目】材料一:如图1,由课本91页例2画函数y=﹣6x与y=﹣6x+5可知,直线y=﹣6x+5可以由直线y=﹣6x向上平移5个单位长度得到由此我们得到正确的结论一:在直线L1:y=K1x+b1与直线L2:y=K2x+b2中,如果K1=K2 且b1≠b2 ,那么L1∥L2,反过来,也成立.
材料二:如图2,由课本92页例3画函数y=2x﹣1与y=﹣0.5x+1可知,利用所学知识一定能证出这两条直线是互相垂直的.由此我们得到正确的结论二:在直线L1:y=k1x+b1 与L2:y=k2x+b2 中,如果k1·k2=-1那么L1⊥L2,反过来,也成立
应用举例
已知直线y=﹣![]() x+5与直线y=kx+2互相垂直,则﹣
x+5与直线y=kx+2互相垂直,则﹣![]() k=﹣1.所以k=6
k=﹣1.所以k=6
解决问题
(1)请写出一条直线解析式______,使它与直线y=x﹣3平行.
(2)如图3,点A坐标为(﹣1,0),点P是直线y=﹣3x+2上一动点,当点P运动到何位置时,线段PA的长度最小?并求出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎军运会,武汉市对城区主干道进行绿化,计划把某一段公路的两侧全部栽上银杏树,要求每两棵树的间隔相等,并且路的每一侧的两端都各栽一棵,如果每隔4米栽一棵,则还差102棵;如果每隔5米栽一棵,则多出102棵,设公路长x米,有y棵树,则下列方程中:①2(![]() +1)﹣102=2(
+1)﹣102=2(![]() +1)+102;②
+1)+102;②![]() ﹣102=
﹣102=![]() +102;③4(
+102;③4(![]() ﹣1)=5(
﹣1)=5(![]() ﹣1);④4(
﹣1);④4(![]() ﹣1)=5(
﹣1)=5(![]() ﹣1),其中正确的是( )
﹣1),其中正确的是( )
A.①③B.②③C.①④D.①
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;
②方程![]() 的两个根是x1=﹣1,x2=3;
的两个根是x1=﹣1,x2=3;
③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题
(1)(﹣2.4)+(﹣3.7)+(﹣4.6)+5.7
(2)﹣20+(﹣14)﹣(﹣18)﹣13
(3)![]()
(4)(﹣3![]() )+12.5+(16
)+12.5+(16![]() )﹣(﹣2.5)
)﹣(﹣2.5)
(5)0.75+0.125+(﹣2![]() )﹣(﹣12
)﹣(﹣12![]() )+(﹣4
)+(﹣4![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com