
����Ŀ��ijУѧ����ѧ��ȤС��Ϊ�˽ⱾУͬѧ���Ͽ��ⲹϰ���̬�ȣ���ѧУ��ȡ�˲���ͬѧ�������ʾ����飬����ֱ�Ϊ��A���dz���ͬ������B����ͬ������C������ν������D������ͬ��������̬�ȣ��ֽ�����ͳ�ƽ���Ƴ�����ͼ����ͳ��ͼ����������ͳ��ͼ���ش��������⣺
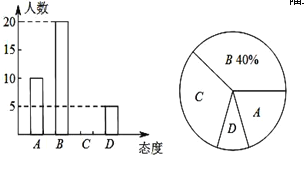
��1����ȡ�˶�����ͬѧ�������ʾ�������
��2���벹ȫ����ͳ��ͼ��
��3���֡�����ͬ��̬�ȵ�ѧ�������İٷֱ���ռ���ε�Բ�Ľ�Ϊ�� ���ȣ�
��4������У��3000��ѧ����������Ƹ�Уѧ���Գ֡���ͬ���͡��dz���ͬ������̬�ȵ�����֮�ͣ�
���𰸡���1��50����2����ͼ����������3��36����4��1800�ˣ�
����������1������ͬ������20����ռ40%�������������������
��2����������-�dz���ͬ-��ͬ-����ͬ�������������ν������������������ͳ��ͼ����������
��3���������������ռ�������İٷ�������������õİٷֱȳ���360�㼴�ɣ�
��4���������ͬ�������dz���ͬ������̬�ȵ�������ռ�İٷ��������������������˼����㼴��.
��1��20��40%=50���ˣ���
��2����ȫ����ͳ��ͼ��ͼ��ʾ��
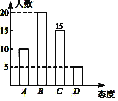
��3����������ռ�������İٷ���Ϊ![]() ��100%=10%��
��100%=10%��
�֡�����ͬ��̬�ȵ�ѧ�������İٷֱ���ռ���ε�Բ�Ľ�Ϊ10%��360��=36�㣬
�ʴ�Ϊ��36��
��4������ͬ���͡��dz���ͬ������̬�ȵ�������ռ�İٷ���Ϊ![]() ��100%=60%��
��100%=60%��
���Уѧ���Ը�ĸ���������֡���ͬ���͡��dz���ͬ������̬�ȵ�����֮��Ϊ3000��60%=1800���ˣ���


 ϰ�⾫ѡϵ�д�
ϰ�⾫ѡϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ڵȱ�������ABC�У�CDΪ���ߣ���Q���߶�CD���˶������߶�QA�Ƶ�Q˳ʱ����ת��ʹ�õ�A�Ķ�Ӧ��E��������BC�ϣ�����BQ�����DAQ=��
��0�㣼����60��������30�㣩.
��1����0�㣼����30��ʱ��
����ͼ1�������⻭��ͼ�Σ������BQE���ú�����ʽ�ӱ�ʾ����
��̽���߶�CE��AC��CQ֮���������ϵ��������֤����
��2����30�㣼����60��ʱ��ֱ��д���߶�CE��AC��CQ֮���������ϵ.


![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ����
A. �����콵��ĸ�����80%����ʾ������80%��ʱ�䶼�ڽ���
B. ����һöӲ�����泯�ϵĸ���Ϊ![]() ����ʾÿ��2�ξ���һ�����泯��
����ʾÿ��2�ξ���һ�����泯��
C. ����Ʊ�н��ĸ���Ϊ1%����ʾ��100�Ų�Ʊ�϶����н�
D. ����һö���������ӣ����ϵĵ���Ϊ2�ĸ���Ϊ![]() ����ʾ�����������������ӣ����׳����ϵĵ���Ϊ2����һ�¼�������Ƶ���ȶ���
����ʾ�����������������ӣ����׳����ϵĵ���Ϊ2����һ�¼�������Ƶ���ȶ���![]() ����
����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0����ͼ����ͼ�����������ĸ����ۣ���4ac��b2��0����4a+c��2b����3b+2c��0����m��am+b��+b��a��m�٩�1����������ȷ���۵ĸ����ǣ�����

A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һЩ��ͬ�ķ�����Ҫ��ˢǽ�森һ��3��һ������ȥ��ˢ8������,���������50m2ǽ��δ���ü���ˢ;ͬ��ʱ����5������������ˢ��10������֮��,�����ˢ�������40m2ǽ�森ÿ��һ�������ȶ�������һ����ˢ12m2ǽ�棬��һ��һ��������һ����������ÿ���ˢ��ǽ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����������һ�ֲ�Ʒ,���ֲ�Ʒ�ijɱ���Ϊ10Ԫ/ǧ��,��֪���ۼ۲����ڳɱ���,����۲��Ź涨���ֲ�Ʒ�����ۼ۲�����18Ԫ/ǧ��,�г����鷢��,�ò�Ʒÿ���������y(ǧ��)�����ۼ�x(Ԫ/ǧ��)֮��ĺ�����ϵ��ͼ��ʾ:
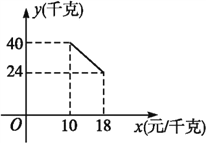
��1����y��x֮��ĺ�����ϵʽ,��д���Ա���x��ȡֵ��Χ;
��2����ÿ�����������W(Ԫ)�����ۼ�x(Ԫ/ǧ��)֮��ĺ�����ϵʽ.�����ۼ�Ϊ����ʱ,ÿ��������������?��������Ƕ���?
��3���þ�������Ҫÿ����168Ԫ����������,���ۼ�Ӧ��Ϊ����?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��һ����Ϊ4a����Ϊb�ij����Σ���ͼ�������ü���ƽ���ֳ��Ŀ�С�����Σ�Ȼ�����Ŀ�С������ƴ�ɵ�һ�������Ρ������Σ���ͼ2����
��ͼ2�е���Ӱ���ֵ����Ϊ ��
�ڹ۲�ͼ2����д�� ��a+b��2����a��b��2��ab֮��ĵ�����ϵ�� ��
�۸��ݣ�2���еĽ��ۣ���x+y=5��xy=![]() ����x��y��2= ��
����x��y��2= ��
��ʵ����ͨ������ͼ�ε��������̽����Ӧ�ĵ�ʽ��
��ͼ3���㷢�ֵĵ�ʽ�� ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���۵�����ֽƬABCD��ʹ��A��D���Ӧ�߹���C������B��60�㣬AB��2����A��E��ABʱ��AE�ij��ǣ�������

A.2![]() B.2
B.2![]() C.
C.![]() D.1+
D.1+![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪˫����![]() ��ֱ��
��ֱ��![]() �ཻ��A��B���㣮��һ�����ϵĵ�M��m��n������A����ࣩ��˫����
�ཻ��A��B���㣮��һ�����ϵĵ�M��m��n������A����ࣩ��˫����![]() ���Ķ��㣮����B��BD��y�ύx���ڵ�D����N��0����n����NC��x�ύ˫����
���Ķ��㣮����B��BD��y�ύx���ڵ�D����N��0����n����NC��x�ύ˫����![]() �ڵ�E����BD�ڵ�C��
�ڵ�E����BD�ڵ�C��
��1������D�����ǣ���8��0������A��B����������k��ֵ��
��2����B��CD���е㣬�ı���OBCE�����Ϊ4����ֱ��CM�Ľ���ʽ��
��3����ֱ��AM��BM�ֱ���y���ཻ��P��Q���㣬��MA=pMP��MB=qMQ����p��q��ֵ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com