练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知一张三角形纸片如图甲，其中将纸片沿过点B的直线折叠，使点C落到AB边上的E点处，折痕为如图乙再将纸片沿过点E的直线折叠，点A恰好与点D重合，折痕为如图丙原三角形纸片ABC中，的大小为______

    【答案】72;

    【解析】

    根据题意设∠A为x,再根据翻折的相关定义得到∠A的大小，随之即可解答.

    设∠A为x，则由翻折对应角相等可得∠EDA=∠A=x，

    由∠BED是△AED的外角可得∠BED=∠EDA+∠A=2x，

    则由翻折对应角相等可得∠C=∠BED=2x，

    因为AB=AC，所以∠ABC=∠C=2x，

    在△ABC中，∠ABC+∠C+∠A=2x+2x+x=180°，

    所以x=36°，

    则∠ABC=2x=72°.

    故本题正确答案为72°.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，⊙O的直径AD长为6，AB是弦，∠A=30°，CD∥AB，且CD= ．
    （1）求∠C的度数；
    （2）求证：BC是⊙O的切线；
    （3）求阴影部分面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

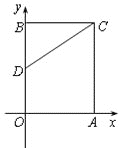
    【题目】如图，在平面直角坐标系中，长方形的顶点在坐标原点，顶点分别在轴，轴的正半轴上，，为边的中点，是边上的一个动点，当的周长最小时，点的坐标为_________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了解本校七年级同学在双休日参加体育锻炼的时间，课题小组进行了问卷调查（问卷调查表如下图所示），并用调查结果绘制了图1、图2两幅统计图（均不完整），请根据统计图解答以下问题.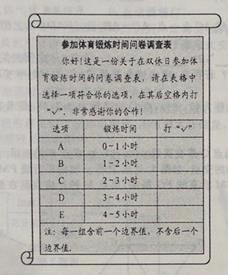



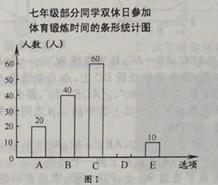
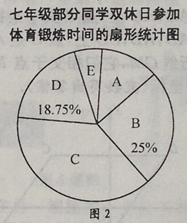
    （1）本次接受问卷调查的同学有多少人？补全条形统计图.
    （2）本校有七年级同学800人，估计双休日参加体育锻炼时间在3小时以内（不含3小时）的人数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小龙在学校组织的社会调查活动中负责了解他所居住的小区450户居民的家庭收入情况. 他从中随机调查了40户居民家庭收入情况（收入取整数，单位：元），并绘制了如下的频数分布表和频数分布直方图.

    分组

    频数

    百分比

    600≤＜800

    2

    5％

    800≤＜1000

    6

    15％

    1000≤＜1200

    45％

    9

    22.5％

    1600≤＜1800

    2

    合计

    40

    100％

    根据以上提供的信息，解答下列问题：

    （1）补全频数分布表.

    （2）补全频数分布直方图.

    （3）绘制相应的频数分布折线图.

    （4）请你估计该居民小区家庭属于中等收入（大于1000不足1600元）的大约有多少户？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在每个小正方形的边长为 的网格图形中，每个小正方形的顶点称为格点．从一个格点移动到与之相距 的另一个格点的运动称为一次跳马变换．例如，在 的正方形网格图形中（如图1），从点 经过一次跳马变换可以到达点 ， ， ， 等处．现有 的正方形网格图形（如图2），则从该正方形的顶点 经过跳马变换到达与其相对的顶点 ，最少需要跳马变换的次数是（ ）

    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】周末，老师带同学去北京植物园中的一二﹒九运动纪念广场，这里有三座侧面为三角形的纪念亭，挺拔的建筑线条象征青年朝气蓬勃、积极向上的精神．基于纪念亭的几何特征，同学们编拟了如下的数学问题：

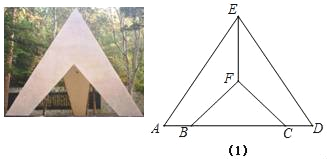
    如图1，点A，B，C，D在同一条直线上，在四个论断“EA=ED，EF⊥AD，AB=DC，FB=FC”中选择三个作为已知条件，另一个作为结论，构成真命题（补充已知和求证），并进行证明．

    已知：如图，点A，B，C，D在同一条直线上，　 　．

    求证：　 　．

    证明：　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面材料：两位同学在用标有数字1，2，...，9的9张卡片做游戏.

    甲同学：“你先从这9张卡片中随意抽取两张（按抽取的先后顺序分别称为“卡片”和“卡片”），别告诉我卡片上是什么数字，然后你把卡片上的数字乘以5，加上7，再乘以2，再加上卡片上的数字，把最后得到的数的值告诉我，我就能猜出你抽出的是哪两张卡片啦！”

    乙同学：“这么神奇？我不信.”

    ……

    试验一下：

    （1）如果乙同学抽出的卡片上的数字为2，卡片上的数字为5，他最后得到的数等于多少；

    （2）若乙同学最后得到的数，则卡片上的数字为多少，卡片上的数字为多少.

    解密：

    请你说明：对任意告知的数，甲同学是如何猜到卡片的.

    解：（1）等于多少.

    （2）若，则卡片上的数字为多少，卡片上的数字为多少.

    解密：

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】课题学习：设计概率模拟实验． 在学习概率时，老师说：“掷一枚质地均匀的硬币，大量重复实验后，正面朝上的概率约是 ．”小海、小东、小英分别设计了下列三个模拟实验：
    小海找来一个啤酒瓶盖（如图1）进行大量重复抛掷，然后计算瓶盖口朝上的次数与总次数的比值；
    小东用硬纸片做了一个圆形转盘，转盘上分成8个大小一样的扇形区域，并依次标上1至8个数字（如图2），转动转盘10次，然后计算指针落在奇数区域的次数与总次数的比值；
    小英在一个不透明的盒子里放了四枚除颜色外都相同的围棋子（如图3），其中有三枚是白子，一枚是黑子，从中随机同时摸出两枚棋子，并大量重复上述实验，然后计算摸出的两枚棋子颜色不同的次数与总次数的比值．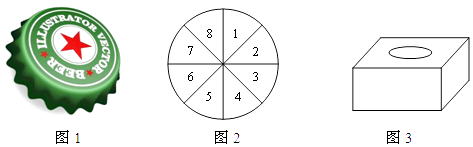

    根据以上材料回答问题：
    小海、小东、小英三人中，哪一位同学的实验设计比较合理，并简要说出其他两位同学实验的不足之处．

    查看答案和解析>>

    同步练习册答案