
【题目】如图,已知 BF=CE,∠B=∠E,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
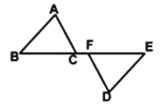
A. AB=DE B. AC∥DF C. ∠A=∠D D. AC=DF
【答案】D
【解析】
根据全等三角形的判定定理分别进行分析即可.
A.∵BF=CE,∴BF-CF=CE-CF,即BC=EF.
∵∠B=∠E,AB=DE,∴ABC≌DEF(SAS),故A不符合题意.
B.∵AC∥DF,∴∠ACE=∠DFC,∴∠ACB=∠DFE(等角的补角相等)
∵BF=CE,∠B=∠E,∴BF-CF=CE-CF,即BC=EF,∴ABC≌DEF(ASA),故B不符合题意.
C.∵BF=CE,∴BF-CF=CE-CF,即BC=EF.
而∠A=∠D,∠B=∠E,∴ABC≌DEF(AAS),故C不符合题意.
D.∵BF=CE,∴BF-CF=CE-CF,即BC=EF,而AC=DF,∠B=∠E,三角形中,有两边及其中一边的对角对应相等,不能判断两个三角形全等,故D符合题意.
故选D.


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3,E、F分别是AB、CD上的点,且∠CFE=60°,将四边形BCFE沿EF翻折,得到B′C′FE,C′恰好落在AD边上,B′C′交AB于点G,则GE的长是( ) 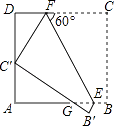
A.3 ![]() ﹣4
﹣4
B.4 ![]() ﹣5
﹣5
C.4﹣2 ![]()
D.5﹣2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,小明购买一种笔记本所付款金额y(元)与购买量x(本)之间的函数图象由线段OB和射线BE组成,则一次购买8个笔记本比分8次购买每次购买1个可节省元. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家门前有一条小河,村里准备在河面上架上一座桥,但河宽AB无法直接测量,爱动脑的小明想到了如下方法:在与AB垂直的岸边BF上取两点C、D使CD= ,再引出BF的垂线DG,在DG上取一点E,并使A、C、E在一条直线上,这时测出线段 的长度就是AB的长.
(1)按小明的想法填写题目中的空格;
(2)请完成推理过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
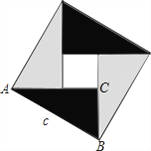
【题目】中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展.现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中,∠ACB=90°,若![]() ,请你利用这个图形解决下列问题:
,请你利用这个图形解决下列问题:
(1)试说明![]() ;
;
(2)如果大正方形的面积是10,小正方形的面积是2,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示:要设计一副宽20厘米、长30厘米的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为2:3,如果要使所有彩条所占面积为原矩形图案面积的![]() ,那么横彩条的宽度为多少厘米,竖彩条的宽度为多少厘米?
,那么横彩条的宽度为多少厘米,竖彩条的宽度为多少厘米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,AB=8. 
(1)利用尺规,作∠CAB的平分线,交⊙O于点D;(保留作图痕迹,不写作法)
(2)在(1)的条件下,连接CD,OD,若AC=CD,求∠B的度数;
(3)在(2)的条件下,OD交BC于点E,求由线段ED,BE, ![]() 所围成区域的面积.(其中
所围成区域的面积.(其中 ![]() 表示劣弧,结果保留π和根号)
表示劣弧,结果保留π和根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com