
【题目】如图在△ABC中,AB=AC=13,BC=10,D是AB的中点,过点D作DE⊥AC于点E,

求:(1)△ABC的面积;
(2)DE的长?
 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O,若∠1=38°,则∠BDE的度数为( )

A. 71° B. 76° C. 78° D. 80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知 BF=CE,∠B=∠E,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
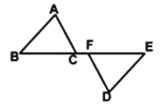
A. AB=DE B. AC∥DF C. ∠A=∠D D. AC=DF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,黔南州近期举办了中小学生“国学经典大赛”.比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式分“单人组”和“双人组”.
(1)小丽参加“单人组”,她从中随机抽取一个比赛项目,恰好抽中“三字经”的概率是多少?
(2)小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则恰好小红抽中“唐诗”且小明抽中“宋词”的概率是多少?请用画树状图或;列表的方法进行说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现有一个面积为150平方米的长方形养鸡场,鸡场的一边靠墙(墙长18米),另三边用竹篱笆围成,在与墙平行的一边,开一扇2米宽的门.如果竹篱笆的长为33米,求这个长方形养鸡场与墙垂直的边长是多少?与墙平行的边长是多少?(列方程解答)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是边长为4的正方形,点P为OA边上任意一点(与点O、A不重合),连接CP,过点P作PM⊥CP交AB于点D,且PM=CP,过点M作MN∥AO,交BO于点N,连结ND、BM,设OP=t.
(1)求点M的坐标(用含t的代数式表示);
(2)试判断线段MN的长度是否随点P的位置的变化而改变?并说明理由.
(3)当t为何值时,四边形BNDM的面积最小;
(4)在x轴正半轴上存在点Q,使得△QMN是等腰三角形,请直接写出不少于4个符合条件的点Q的坐标(用含t的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,我们在“格点”直角坐标系上可以看到,要求AB或CD的长度,可以转化为求Rt△ABC或Rt△DEF的斜边长.
例如:从坐标系中发现:D(﹣7,3),E(4,﹣3),所以DF=|5﹣(﹣3)|=8,EF=|4﹣(﹣7)|=11,所以由勾股定理可得:DE=![]() .
.
(1)在图①中请用上面的方法求线段AB的长:AB= ;
(2)在图②中:设A(x1,y1),B(x2,y2),试用x1,x2,y1,y2表示:AC= ,BC= ,AB= ;
(3)试用(2)中得出的结论解决如下题目:已知:A(2,1),B(4,3);
①直线AB与x轴交于点D,求线段BD的长;
②C为坐标轴上的点,且使得△ABC是以AB为边的等腰三角形,请求出C点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)请画出△ABC关于y轴对称的△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点,不写画法);
(2)直接写出A′,B′,C′三点的坐标:A′( ),B′( ),C′( )
(3)计算△ABC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com