
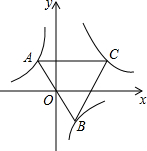
 如图,已知点A是双曲线y=-$\frac{2}{x}$在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第一象限内,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$(k>0)上运动,则k的值是6.
如图,已知点A是双曲线y=-$\frac{2}{x}$在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第一象限内,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$(k>0)上运动,则k的值是6. 分析 设点A的坐标为(a,-$\frac{2}{a}$),连接OC,则OC⊥AB,表示出OC,过点C作CD⊥x轴于点D,设出点C坐标,在Rt△OCD中,利用勾股定理可得出x2的值,继而得出y与x的函数关系式.
解答  解:设A(a,-$\frac{2}{a}$),
解:设A(a,-$\frac{2}{a}$),
∵点A与点B关于原点对称,
∴OA=OB,
∵△ABC为等边三角形,
∴AB⊥OC,OC=$\sqrt{3}$AO,
∵AO=$\sqrt{{a}^{2}+({\frac{2}{a})}^{2}}$,
∴CO=$\sqrt{3}$AO=$\sqrt{3{a}^{2}+\frac{12}{{a}^{2}}}$,
过点C作CD⊥x轴于点D,
则可得∠BOD=∠OCD(都是∠COD的余角),
设点C的坐标为(x,y),则tan∠BOD=tan∠OCD,即$\frac{\frac{2}{a}}{a}$=$\frac{x}{y}$,
解得:y=$\frac{{a}^{2}}{2}$x,
在Rt△COD中,CD2+OD2=OC2,即y2+x2=3a2+$\frac{12}{{a}^{2}}$,
将y=$\frac{{a}^{2}}{2}$x代入,可得:x2=$\frac{12}{{a}^{2}}$,
故x=$\frac{2\sqrt{3}}{a}$,y=$\sqrt{3}$a,
则k=xy=6,
故答案为:6.
点评 本题考查了反比例函数的综合题,涉及了解直角三角形、等边三角形的性质及勾股定理的知识,综合考察的知识点较多,解答本题的关键是将所学知识融会贯通,注意培养自己解答综合题的能力.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
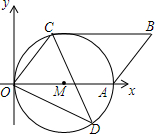 如图,在平面直角坐标系xOy中,点A在x轴正半轴上,OA=8,以OA为直径作⊙M,点C在⊙M上,∠AOC=45°,四边形ABCO为平行四边形.
如图,在平面直角坐标系xOy中,点A在x轴正半轴上,OA=8,以OA为直径作⊙M,点C在⊙M上,∠AOC=45°,四边形ABCO为平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
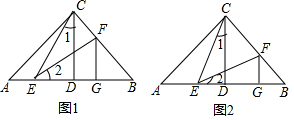 【问题情境】一节数学课后,老师布置了一道课后练习题:
【问题情境】一节数学课后,老师布置了一道课后练习题: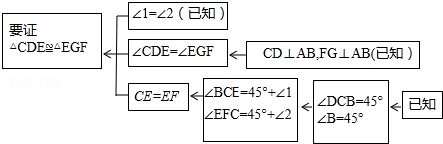
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com