
 �������龳��һ����ѧ�κ���ʦ������һ���κ���ϰ�⣺
�������龳��һ����ѧ�κ���ʦ������һ���κ���ϰ�⣺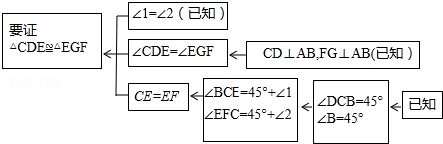
���� ��1�����ݿ�ͼ�е�˼·��������д�����̼��ɣ�
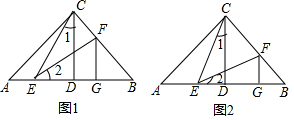
��2������֤����ACE=��2��Ȼ��֤����ACE�ա�BEF������ȫ�������εĶ�Ӧ����ȼ���֤�ã�
��� ֤������1����AC=BC����ACB=90�㣬CD��AB�ڵ�D��
���DCB=��B=45�㣬
�֡ߡ�BCE=��DCB+��1����EFC=��B+��2����1=��2��
���BCE=��EFC��
��CE=EF��
�ڡ�CDE�͡�EGF�У�
$\left\{\begin{array}{l}{��1=��2}\\{��CDE=��EGF}\\{CE=EF}\end{array}\right.$��
���CDE�ա�EGF��
��2����CEƽ�֡�ACD��
���ACE=��1��
�֡ߡ�1=��2��
���ACE=��2��
�ڡ�ACE�͡�BEF�У�
$\left\{\begin{array}{l}{��A=��B}\\{��ACE=��2}\\{CE=EF}\end{array}\right.$��
���ACE�ա�BEF��
��AE=BF��
���� ���⿼���������ε�ȫ�ȵ��ж������ʣ��Լ����������ε��ж������ʣ�֤��CE=EF�DZ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
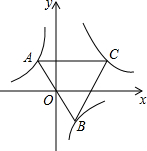 ��ͼ����֪��A��˫����y=-$\frac{2}{x}$�ڵڶ�����֧�ϵ�һ�����㣬����AO���ӳ�����һ��֧�ڵ�B����ABΪ�����ȱ�������ABC����C�ڵ�һ�����ڣ����ŵ�A���˶�����C��λ��Ҳ���ϱ仯������Cʼ����˫����y=$\frac{k}{x}$��k��0�����˶�����k��ֵ��6��
��ͼ����֪��A��˫����y=-$\frac{2}{x}$�ڵڶ�����֧�ϵ�һ�����㣬����AO���ӳ�����һ��֧�ڵ�B����ABΪ�����ȱ�������ABC����C�ڵ�һ�����ڣ����ŵ�A���˶�����C��λ��Ҳ���ϱ仯������Cʼ����˫����y=$\frac{k}{x}$��k��0�����˶�����k��ֵ��6���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-3��2�� | B�� | ��3��2�� | C�� | ��-3��-2�� | D�� | ��3��-2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
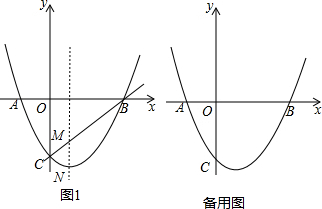
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com