练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

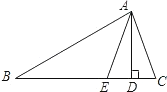
    【题目】在△ABC中，AD是BC边上的高，AE是角平分线，∠B=30°，∠C=70°，求∠CAD和∠DAE的度数．

    【答案】∠CAD=20°, ∠DAE=20°

    【解析】

    在Rt△ACD中，利用直角三角形两锐角互余即可求出∠CAD；
    根据三角形的内角和等于180°列式求出∠BAC，再根据角平分线的定义求出∠CAE，然后列式计算即可求出∠DAE．

    解：∵AD是BC边上的高

    ∴∠ADC=90°

    在Rt△ADC中，∠C=70°

    ∴∠CAD=90°-∠C=90°-70°=20°

    在△ABC中

    ∵∠B=30°，∠C=70°

    ∴∠BAC=180°-∠B-∠C=180°-30°-70°=80°

    ∵AE平分∠BAC

    ∴∠CAE=∠BAC=×80°=40°

    ∴∠DAE=∠CAE﹣∠CAD=40°﹣20°=20°

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某家电商场计划用9万元从生产厂家购进50台电视机，已知该厂家生产3种不同型号的电视机，出厂价分别为A种每台1500元，B种每台2100元，C种每台2500元．

    （1）若家电商场同时购进两种不同型号的电视机共50台，用去9万元，请你计算一下商场有哪几种进货方案？

    （2）若商场销售一台A种电视机可获利150元，销售一台B种电视机可获利200元，销售一台C种电视机可获利250元，在同时购进两种不同型号的电视机方案中，为了使销售时获利最多，应选择哪种方案？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE内时，∠A与∠1＋∠2之间有始终不变的关系是__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】综合与探究

    阅读理解：数轴是学习有理数的一种重要工具，任何有理数都可以用数轴上的点表示，这样能够运用数形结合的方法解决一些问题.例如，两个有理数在数轴上对应的点之间的距离可以用较大数与较小数的差来表示.例如：

    在数轴上，有理数3与1对应的两点之间的距离为；

    在数轴上，有理数3与－2对应的两点之间的距离为；

    在数轴上，有理数－3与－2对应的两点之间的距离为.

    解决问题：如图所示，已知点表示的数为－3，点表示的数为－1，点表示的数为2.

    （1）点和点之间的距离为______.

    （2）若数轴上动点表示的数为，当时，点和点之间的距离可表示为______；当时，点和点之间的距离可表示为______.

    （3）若数轴上动点表示的数为，点在点和点之间，点和点之间的距离表示为，点和点之间的距离表示为，求（用含的代数式表示并进行化简）

    （4）若数轴上动点表示的数为－2，将点向右移动19个单位长度，再向左移动23个单位长度终点为，那么，两点之间的距离是______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，等腰三角形ABC的底边BC在x轴正半轴上，点A在第一象限，延长AB交y轴负半轴于点D，延长CA到点E，使AE=AC，双曲线y= （x＞0）的图象过点E．若△BCD的面积为2 ，则k的值为（ ）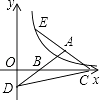

    A.4
    B.4
    C.2
    D.2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知长方形纸片ABCD，点E在边AB上，点F、G在边CD上，连接EF、EG．将∠BEG对折，点B落在直线EG上的点B′处，得折痕EM；将∠AEF对折，点A落在直线EF上的点A′处，得折痕EN．

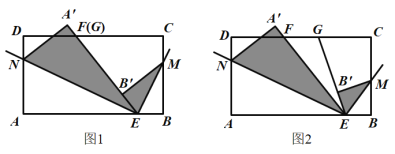
    （1）如图1，若点F与点G重合，求∠MEN的度数；

    （2）如图2，若点G在点F的右侧，且∠FEG＝30°，求∠MEN的度数；

    （3）若∠MEN＝α，请直接用含α的式子表示∠FEG的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点B在线段AC上，点D在线段AB上．

    （1）如图1，若AB=6cm，BC=4cm，D为线段AC的中点，求线段DB的长度；

    （2）如图2，若BD=AB=CD，E为线段AB的中点，EC=12cm，求线段AC的长度．

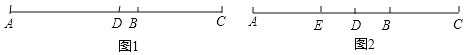
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，的三个顶点都在格点上，点的坐标为．

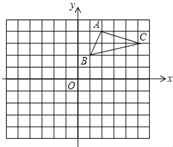
    （1）画出关于轴对称的，并写出点的坐标　 　．

    （2）画出绕原点旋转后得到的，并写出点的坐标 　．

    （3）是否为直角三角形？答　 　（填是或者不是）．

    （4）利用格点图，画出边上的高，并求出的长，　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，点D在AB的延长线上，DC切⊙O于点C，若∠A=25°，则∠D等于（ ）

    A.20°
    B.30°
    C.40°
    D.50°

    查看答案和解析>>

    同步练习册答案