
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 于点
于点![]() ,
,![]() 的平分线分别交
的平分线分别交![]() 、
、![]() 于
于![]() 、
、![]() 两点,
两点,![]() 为
为![]() 的中点,
的中点,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,连接
,连接![]() ,下列结论:①
,下列结论:①![]() 为等腰三角形;②
为等腰三角形;②![]() ;③
;③![]() ;④
;④![]() .其中正确的结论有( )
.其中正确的结论有( )

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
【答案】D
【解析】
①由等腰直角三角形的性质得∠BAD=∠CAD=∠C=45°,再根据三角形外角性质可得到∠AEF=∠AFE,可判断△AEF为等腰三角形,于是可对①进行判断;求出BD=AD,∠DBF=∠DAN,∠BDF=∠ADN,证△DFB≌△DAN,即可判断②③;连接EN,只要证明△ABE≌△NBE,即可推出∠ENB=∠EAB=90°,由此可知判断④.
解:∵等腰Rt△ABC中,∠BAC=90°,AD⊥BC,
∴∠BAD=∠CAD=∠C=45°,BD=AD,
∵BE平分∠ABC,
∴∠ABE=∠CBE=![]() ∠ABC=22.5°,
∠ABC=22.5°,
∴∠AEF=∠CBE+∠C=22.5°+45°=67.5°,
∠AFE=∠FBA+∠BAF=22.5°+45°=67.5°,
∴∠AEF=∠AFE,
∴AF=AE,即△AEF为等腰三角形,所以①正确;
∵![]() 为
为![]() 的中点,
的中点,
∴AM⊥BE,
∴∠AMF=∠AME=90°,
∴∠DAN=90°67.5°=22.5°=∠MBN,
在△FBD和△NAD中
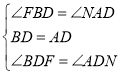 ,
,
∴△FBD≌△NAD(ASA),
∴DF=DN,AN=BF,所以②③正确;
∵AM⊥EF,
∴∠BMA=∠BMN=90°,
∵BM=BM,∠MBA=∠MBN,
∴△MBA≌△MBN,
∴AM=MN,
∴BE垂直平分线段AN,
∴AB=BN,EA=EN,
∵BE=BE,
∴△ABE≌△NBE,
∴∠ENB=∠EAB=90°,
∴EN⊥NC,故④正确,
故选:D.


科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队计划修建一条长15千米的乡村公路,已知甲工程队每天比乙工程队每天多修路0.5千米,乙工程队单独完成修路任务所需天数是甲工程队单独完成修路任务所需天数的1.5倍.
(1)求甲、乙两个工程队每天各修路多少千米?
(2)若甲工程队每天的修路费用为0.5万元,乙工程队每天的修路费用为0.4万元,要使两个工程队修路总费用不超过5.2万元,甲工程队至少修路多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )

A.一处B.二处C.三处D.四处
查看答案和解析>>
科目:初中数学 来源: 题型:
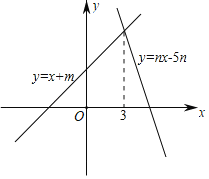
【题目】如图,直线y=x+m与y=nx﹣5n(n≠0)的交点的横坐标为3,则关于x的不等式x+m>nx﹣5n>0的整数解为( )
A.3B.4C.5D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中央电视台的“中国诗词大赛”节目文化品位高,内容丰富,某校初二年级模拟开展“中国诗词大赛”比赛,对全年级同学成绩进行统计后分为“优秀”、“良好”、“一般”、“较差”四个等级,并根据成绩绘制成如下两幅不完整的统计图,请结合统计图中的信息,回答下列问题:

(1)扇形统计图中“优秀”所对应的扇形的圆心角为 度,并将条形统计图补充完整.
(2)此次比赛有四名同学活动满分,分别是甲、乙、丙、丁,现从这四名同学中挑选两名同学参加学校举行的“中国诗词大赛”比赛,请用列表法或画树状图法,求出选中的两名同学恰好是甲、丁的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
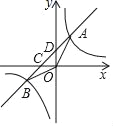
【题目】如图,已知直线y=k1x+b与x轴、y轴相交于C、D两点,与y=![]() 交于A(m,2)、B(﹣2,n)两点.
交于A(m,2)、B(﹣2,n)两点.
(1)求m+n的值;
(2)连接OA、OB,若tan∠AOD+tan∠BOC=1.
①当不等式k1x+b>![]() 时,请结合图象求x的取值范围;
时,请结合图象求x的取值范围;
②设点E在y轴上,且满足∠AEO+∠AOD=45°,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以水![]() 润
润![]() 城,打造
城,打造![]() 四河一库
四河一库![]() 生态水系工程,是巩义坚持不懈推进文明创建与百城提质深度融合的缩影,伊洛河畔正是此项目中的一段.如今,伊洛河畔需要铺设一条长为
生态水系工程,是巩义坚持不懈推进文明创建与百城提质深度融合的缩影,伊洛河畔正是此项目中的一段.如今,伊洛河畔需要铺设一条长为![]() 米的管道,决定由甲、乙两个工程队来完成.已知甲工程队比乙工程队每天能多铺设
米的管道,决定由甲、乙两个工程队来完成.已知甲工程队比乙工程队每天能多铺设![]() 米,且甲工程队铺设
米,且甲工程队铺设![]() 米所用的天数与乙工程队铺设
米所用的天数与乙工程队铺设![]() 米所用的天数相同.(完成任务的工期为整数)
米所用的天数相同.(完成任务的工期为整数)
(1)甲、乙工程队每天各能铺设多少米?
(2)如果要求完成该项管道铺设任务的工期不超过![]() 天,那么为两工程队分配工程量的方案有几种?请你帮助设计出来(工程队分配工程量为整百数)
天,那么为两工程队分配工程量的方案有几种?请你帮助设计出来(工程队分配工程量为整百数)
查看答案和解析>>
科目:初中数学 来源: 题型:
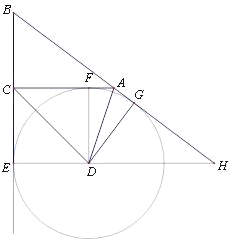
【题目】如图,在△ABC中,BC=a,AC=b,AB=c,⊙D与BC、AC、AB都相切,切点分别是E、F、G,BA、ED的延长线交于点H,a、b是关于x的方程x2﹣(c+4)x+4c+8=0的两个根.
(1)求证:△ABC是直角三角形;
(2)若25asin∠BAC=9c,求四边形CEDF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com