
【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A(1,0),B(3,0)两点,与y轴交于点C,其顶点为点D,点E的坐标为(0,﹣1),该抛物线与BE交于另一点F,连接BC.
(1)求该抛物线的解析式;
(2)一动点M从点D出发,以每秒1个单位的速度沿与y轴平行的方向向上运动,连接OM,BM,设运动时间为t秒(t>0),在点M的运动过程中,当t为何值时,∠OMB=90°?
(3)在x轴上方的抛物线上,是否存在点P,使得∠PBF被BA平分?若存在,请直接写出点P的坐标;若不存在,请说明理由.

【答案】(1)y=﹣![]() x2+
x2+![]() x﹣2;(2)
x﹣2;(2)![]() ﹣
﹣![]() ;(3)P(
;(3)P(![]() ,
, ![]() ).
).
【解析】(1)用待定系数法求出抛物线解析式;
(2)设出点M,用勾股定理求出点M的坐标,从而求出MD,最后求出时间t;
(3)由∠PBF被BA平分,确定出过点B的直线BN的解析式,求出此直线和抛物线的交点即可.
解:(1)∵抛物线y=ax2+bx﹣2(a≠0)与x轴交于A(1,0)、B(3,0)两点,
∴![]() ,
,
∴ ,
,
∴抛物线解析式为y=﹣![]() x2+
x2+![]() x﹣2;
x﹣2;
(2)如图1,
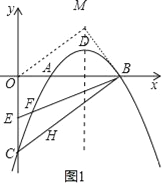
由(1)知y=﹣![]() x2+
x2+![]() x﹣2=﹣
x﹣2=﹣![]() (x﹣2)2+
(x﹣2)2+![]() ;
;
∵D为抛物线的顶点,
∴D(2, ![]() ),
),
∵一动点M从点D出发,以每秒1个单位的速度平沿行与y轴方向向上运动,
∴设M(2,m),(m>![]() ),
),
∴OM2=m2+4,BM2=m2+1,OB2=9,
∵∠OMB=90°,
∴OM2+BM2=OB2,
∴m2+4+m2+1=9,
∴m=![]() 或m=﹣
或m=﹣![]() (舍),
(舍),
∴M(0, ![]() ),
),
∴MD=![]() ﹣
﹣![]() ,
,
∵一动点M从点D出发,以每秒1个单位的速度平沿行与y轴方向向上运动,
∴t=![]() ﹣
﹣;
(3)存在点P,使∠PBF被BA平分,
如图2,
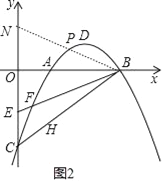
∴∠PBO=∠EBO,
∵E(0,﹣1),
∴在y轴上取一点N(0,1),
∵B(3,0),
∴直线BN的解析式为y=﹣![]() x+1①,
x+1①,
∵点P在抛物线y=﹣![]() x2+
x2+![]() x﹣2②上,
x﹣2②上,
联立①②得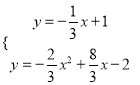 ,
,
解得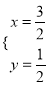 或
或![]() (舍去),
(舍去),
∴P(![]() ,
, ![]() ).
).
“点睛”本题看考查二次函数综合题、待定系数法、一次函数的应用、三角形的面积角平分线等知识,解题时根据灵活运用所学知识,学会构建一次函数,利用方程组求两个函数交点坐标,属于中考常考题型.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A(1,0),B(2,0),正六边形ABCDEF沿x轴正方向无滑动滚动,每旋转60°为滚动1次,那么当正六边形ABCDEF滚动2017次时,点F的坐标是( )

A. (2017,0) B. (2017![]() ,
, ![]() ) C. (2018,
) C. (2018, ![]() ) D. (2018,0)
) D. (2018,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某课外兴趣小组为了解所在地区老年人的健康情况,分别作了四种不同的抽样调查,你认为抽样比较合理的是( )
A. 调查了10名老年邻居的健康状况
B. 在医院调查了1000名老年人的健康状况
C. 在公园调查了1000名老年人的健康状况
D. 利用派出所的户籍网随机调查了该地区10%的老年人的健康状况
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.如果两条直线被第三条直线所截,那么内错角相等
B.过一点有且仅有一条直线与已知直线垂直
C.过直线外一点有且只有一条直线与已知直线平行
D.同一平面内两条线段不平行必相交
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在端午节到来之前,学校食堂推荐了A,B,C三家粽子专卖店,对全校师生爱吃哪家店的粽子作调查,以决定最终向哪家店采购,下面的统计量中最值得关注的是( )
A.方差
B.平均数
C.中位数
D.众数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com